Senza staccare la penna dal foglio
Cari amici, in questo articolo vi propongo alcuni classici puzzles che chiedono di tracciare un disegno con un unico tratto di penna e senza ripassare su una linea già tracciata. Ne parliamo anche qui.
- Come riconoscere facilmente i disegni possibili e quelli impossibili?
- Come individuare un punto buono da cui iniziare un disegno?
Un teorema di Eulero, facile da capire, ci aiuta a rispondere a queste domande e a risolvere questi puzzles.
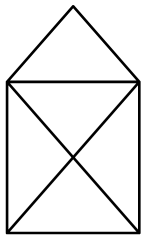
1. Uno facile: la casetta
Sapreste disegnare la figura qui sotto senza mai staccare la penna dal foglio e percorrendo ogni segmento una sola volta?
2. Uno impossibile: il rettangolo con le diagonali
È possibile disegnare un rettangolo e le sue diagonali con un solo tratto di penna percorrendo tutti i segmenti, ma ciascuno una sola volta?
I grafi e il teorema di Eulero
Una figura di questo tipo, formata da punti (A, B, C, D, E, F) e da linee che li congiungono, si chiama grafo.
- I punti A, B, C, D ecc. si chiamano nodi del grafo.
- Le linee AB, BC, BF ecc. si chiamano archi (o lati o segmenti) del grafo.
- Il numero di archi che escono da un nodo si chiama ordine del nodo.
Per esempio l’ordine del nodo E è 4 mentre l’ordine del nodo D è 3.
Quando si dice “nodo pari” o “nodo dispari” si intende rispettivamente “nodo di ordine pari” o “nodo di ordine dispari”.
Un cammino Euleriano è un percorso su un grafo che attraversa tutti gli archi esattamente una volta.
Tracciare un disegno con un solo tratto di penna senza ripassare su una linea già tracciata equivale a fare un cammino Euleriano in un grafo.
Leonard Euler e Carl Hierholzer hanno dimostrato che è possibile trovare un cammino Euleriano in un grafo alle seguenti condizioni:
- I grafi che hanno tutti i nodi pari si possono tracciare con un tratto continuo partendo da un nodo qualunque e tornando al nodo di partenza (ciclo Euleriano).
- I grafi che hanno esattamente 2 nodi dispari (e tutti gli altri pari) si possono tracciare con un tratto continuo partendo da uno di essi e arrivando all’altro (cammino Euleriano).
- I grafi che hanno più di 2 nodi dispari non hanno un cammino Euleriano.
La figura a forma di casetta si può disegnare partendo dal punto C oppure dal punto D.
Ci sono molte soluzioni possibili (quante?), qui ne riporto due.
È permesso incrociare le linee ma la soluzione in rosso è un esempio senza incroci.
Attenzione. Ho sdoppiato alcuni punti per facilitare la lettura della costruzione. I punti di partenza/arrivo sono segnati con un bollino.
Il rettangolo con le diagonali, invece, ha 4 nodi dispari, perciò non si può tracciare con un unico tratto di penna senza ripassare su una linea già tracciata.
3. Variazioni sul tema
Provate a disegnare le seguenti figure senza mai staccare la penna dal foglio e senza ripassare su una linea già tracciata. È possibile passare più volte sugli incroci.
4. Uno a tre dimensioni: colorare gli spigoli di un ottaedro
Vogliamo colorare tutti gli spigoli di un ottaedro con un pennarello rosso senza mai staccare la punta e senza ripassare su uno spigolo già colorato.
È possibile?
Quale percorso deve seguire la punta del pennarello?
5. Uno col trucco: scrivere 100
È possibile scrivere il numero 100 su un foglio come si vede qui sotto senza mai staccare la punta della penna dal foglio?
6. Altri esercizi
Ecco altri esercizi. Quali sono possibili e quali impossibili?
Risposte & riflessioni
1. Uno facile: la casetta
Altre soluzioni.
2. Uno impossibile: il rettangolo
Come abbiamo già visto, il problema non si può risolvere.
3. Variazioni sul tema
La prima figura ha ha tutti i nodi pari, ciascuno dei quali può essere il punto di partenza di un ciclo Euleriano.
La seconda ha due nodi dispari, perciò si possono trovare diversi cammini Euleriani.
La terza figura ha 4 nodi dispari, quindi non ha soluzioni.
4. Uno a tre dimensioni: colorare gli spigoli di un ottaedro
Possiamo immaginare l’ottaedro come un grafo nello spazio: i vertici sono i nodi, gli spigoli sono gli archi.
Ecco quindi una possibile soluzione.
Tuttavia è più interessante riportare la rete di collegamenti sul piano con un grafo equivalente.
Ciascun nodo ha ordine pari, perciò esiste un percorso chiuso che passa per tutti gli archi.
Nell’ordine il percorso passa per questi vertici: A, C, B, A, E, F, D, E, C, F, B, D, A.
5. Uno col trucco: scrivere 100
Si piega il foglio e si scrive 100 come illustrato nella figura qui sotto.
Si rimette a posto la piegatura ed ecco il risultato.
6. Altri esercizi
I tre esercizi seguenti sono equivalenti e impossibili poiché hanno 4 nodi dispari.
Le tre figure seguenti hanno due nodi dispari, perciò si possono tracciare partendo da uno di essi.
L’ esercizio seguente è impossibile.
Pace e bene a tutti.
GfBo
Continua la lettura su: https://blogdimatematicaescienze.it/senza-staccare-la-penna-dal-foglio/ Autore del post: Blog di Matematica e Scienze Fonte: https://blogdimatematicaescienze.it
