Inversione per raggi vettori reciproci
Geometria delle trasformazioni: bellezza e utilità dell’inversione per raggi vettori reciproci.
In questo articolo l’autore tratta dell’inversione per raggi vettori reciproci.
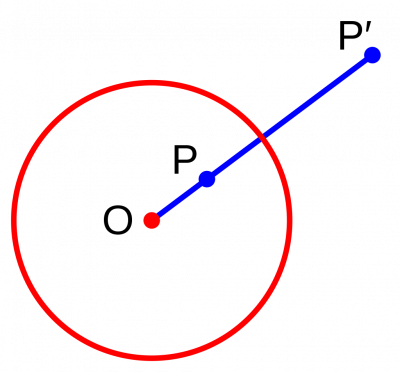
È data una circonferenza k di centro O e raggio r. Ad ogni punto P del suo piano, distinto da O, è possibile associare un punto P’, appartenente alla semiretta di origine O e passante per P, in modo che risulti: OP·OP’=r2
Questa corrispondenza tra i punti P e P’ si definisce inversione (o trasformazione) per raggi vettori reciproci o anche inversione rispetto alla circonferenza k.
L’argomento non rientra nel curricolo della scuola secondaria ed è perciò sconosciuto agli studenti di
quella scuola, ma forse può interessare alcuni di coloro che intendono intraprendere studi universitari in settori in cui la Matematica è disciplina fondamentale.
L’argomento è di per sé interessante ma è anche utile in molte questioni. Cosa che l’autore evidenzia con
alcuni esempi, in cui sono proposti esercizi che si risolvono ricorrendo all’inversione.
Leggi l’articolo
Continua la lettura su: https://www.matmedia.it/inversione-per-raggi-vettori-reciproci/?utm_source=rss&utm_medium=rss&utm_campaign=inversione-per-raggi-vettori-reciproci Autore del post: Matmedia Fonte: http://www.matmedia.it
