Il punto simmediano di un triangolo
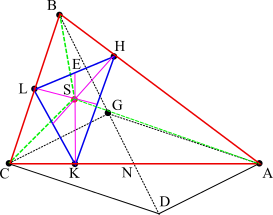
Che cos’è e quali sono le proprietà del punto simmediano di un triangolo (parte prima).
Il punto simmediano di un triangolo coincide con il baricentro del triangolo pedale del punto rispetto al triangolo di riferimento.
Si tratta di un teorema conosciuto come “teorema di Lemoine”. Di recente (2017) si è occupato di esso il giovane matematico vietnamita Tran Quang Hung insegnante di geometria presso la High School for Gifted Students (HSGS) della Vietnam National University ad Hanoi.
L’autore fornisce una dimostrazione del teorema mutuata proprio dalla versione di Hung. Fornisce pure una dimostrazione per via analitica nel caso particolare in cui il triangolo di riferimento è un triangolo rettangolo e una verifica in due casi in cui i triangoli di riferimento hanno vertici assegnati: in uno di tali casi il triangolo di riferimento è acutangolo, nell’altro è ottusangolo.
L’articolo, in particolare nella parte delle verifiche, può offrire ai docenti delle scuole superiori spunti per esercizi interessanti di Geometria Analitica. Ad esso farà seguito una seconda parte di completamento.
Proprietà del punto simmediano (parte prima)
