Punti notevoli del triangolo

I luoghi geometrici descritti dai quattro punti notevoli di un triangolo con proposte di esercizi per gli studenti del primo biennio della Scuola Secondaria di 2° grado.

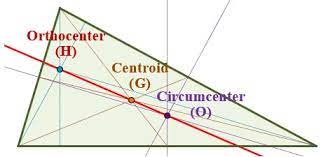
La retta di Eulero

Il presente lavoro è dedicato allo studio dei luoghi geometrici descritti dai quattro punti notevoli di un triangolo quando un vertice percorre, interamente, una circonferenza. Nei primi due casi, il lato fisso del triangolo è esterno alla circonferenza e non ha intersezioni con essa; negli altri due casi, la circonferenza è circoscritta al triangolo stesso.
I problemi nascono dall’osservazione di alcuni disegni elaborati in ambiente Cabri géomètre o Geogebra, dove è possibile valutare alcune rappresentazioni di figure geometriche, anche in modo dinamico.
Gli esercizi presentati potrebbero essere rivolti agli studenti del primo biennio della Scuola Secondaria Superiore e a tutti coloro che trovano interessante questo tipo di attività speculativa, dove le conoscenze di Geometria Elementare e la disponibilità al ragionamento logico sono utilizzati per conseguire risultati non sempre prevedibili. Allo scopo, sono necessarie alcune nozioni contenute in qualsiasi testo di Geometria Piana per il biennio delle Scuole Superiori.
I risultati che si conseguono sono frutto del ragionamento logico, dell’applicazione dei metodi e dei contenuti propri della Geometria Razionale mentre, gli strumenti sono la riga ed il compasso. Lo sviluppo interessato degli esercizi potrebbe rafforzare le capacità di elaborazione del singolo, potenziando anche l’acquisizione dei metodi e dei mezzi per passare da una problematica, di carattere pratico o descrittiva, ad una possibile interpretazione della stessa secondo i canoni formali di una Teoria consolidata,