Fasciando un cubo nel 2024: lo avete risolto?
La settimana scorsa vi ho proposto le seguenti attività da risolvere in classe.
attività 1
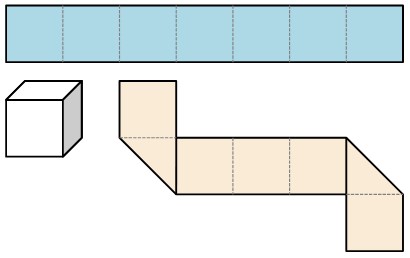
Con una striscia di carta formata da 7 quadrati unitari si può fasciare un cubo unitario.
Come si fa?
Ritagliate una striscia di carta come quella qui sotto e provate a formare un cubo (la sua superficie).
attività 2
Usando 4 di queste strisce provate a formare il numero 2024 come mostrato qui sotto.
Sono ammesse piegature solo lungo i lati o le diagonali dei quadrati.
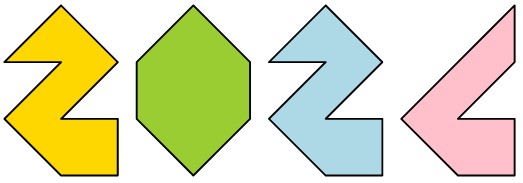
Le avete risolte? Ecco le soluzioni!
attività 1
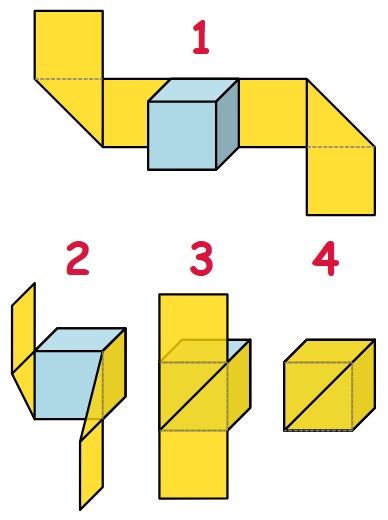
attività 2
Ecco una possibile soluzione per costruire la cifra “2”.
per approfondire
La striscia di 7 quadrati è un esempio di eptomino (o heptomino o 7-omino) e fa parte della grande famiglia dei polimini (in inglese polyominoes).
In queste attività abbiamo imparato a piegare un particolare eptomino per formare la superficie di un cubo e altre forme piane.
Vi propongo alcuni link ad articoli che illustrano quanto sia interessante e attuale il problema cosiddetto del “Folding polyominoes”.
- Folding Polyominoes with Holes into a Cube, recuperabile tramite la ricerca dalla home page dell’Institute of Operating Systems and Computer Networks
- Folding Small Polyominoes into a Unit Cube, recuperabile nella sezione Papers & Books del sito di Erik Demaine
- Folding Polyominoes into (Poly) Cubes, recuperabile tramite la ricerca della home page di DSpace@MIT
- Cube folding, recuperabile nella sezione Mathematical and Puzzle Fonts/Typefaces del sito di Erik Demaine
- FLEX-I-CUBE designed by Philip Noble, recuperabile digitando nella ricerca di un browser la chiave “flexicube thoki yenn”
Foto cover: epsilomo / Shutterstock
Continua la lettura su: https://blogdimatematicaescienze.it/fasciando-un-cubo-nel-2024-lo-avete-risolto/ Autore del post: Fonte:
