La matematica come esplorazione-parte 1
Care colleghe, cari colleghi, in questo articolo vi propongo cinque attività che aiutano a capire come funziona l’esplorazione in Matematica e come è collegata con l’immaginazione e la libertà. Sono adatte a diversi livelli scolastici, a partire dal secondo ciclo della scuola primaria.
Se affrontiamo queste attività con lo spirito dell’esplorazione matematica, arriviamo a sfiorare temi molto interessanti della ricerca contemporanea.
Questo articolo è una relazione dettagliata di un seminario che ho tenuto al 27o Convegno Nazionale “Incontri con la Matematica” – Castel San Pietro Terme (BO) – 2023. Le soluzioni delle singole attività saranno pubblicate nella seconda parte.
1. Esplorazione, avventura, trucchi e fortuna in matematica
Francis Su, nel suo libro Mathematics for human flourishing, ci ha mostrato in che modo la matematica è collegata con alcuni bisogni umani fondamentali come l’esplorazione, il gioco, il combattimento e la libertà. (Su, 2019)
Il libro é stato tradotto in italiano e pubblicato nel 2023. (Su, 2023)
La parola esplorazione ci porta a pensare la matematica come un territorio (oppure un palazzo? un’astronave? un oceano?) da scoprire ma anche da costruire.
Come vi sentite quando cercate di risolvere un problema matematico davvero nuovo per voi?
Provate a confrontarvi con le sensazioni di Maryam Mirzakhani:
“I don’t have any particular recipe,” Mirzakhani said of her approach to developing new proofs. “It is the reason why doing research is challenging as well as attractive. It is like being lost in a jungle and trying to use all the knowledge that you can gather to come up with some new tricks, and with some luck you might find a way out. (Carey, 2014)
[“Non ho particolari ricette“, spiegò Mirzakhani riguardo il suo approccio allo sviluppo di nuove prove. “È come perdersi in una giungla e cercare di usare tutte le conoscenze che puoi mettere insieme per escogitare qualche nuovo trucco, e con un po’ di fortuna potresti trovare una via d’uscita.“]
Secondo questa visione, quando affrontiamo situazioni nuove in matematica e le ricette precostituite non funzionano, abbiamo la libertà di inventare trucchi, modificare le domande e confidare persino nella fortuna.
2. Problemi normali versus compiti di esplorazione
Che differenza c’è tra un normale problema scolastico e una proposta di esplorazione matematica?
La differenza principale è questa: i problemi indicano chiaramente ciò che viene dato e ciò che viene chiesto, mentre le esplorazioni contengono elementi di incertezza o apertura, e richiedono agli studenti un lavoro significativo di interpretazione della situazione e spesso di rielaborazione delle domande. (Da Ponte, 2005, 2014)
Ma forse la vera differenza sta nell’atteggiamento con cui un problema è affrontato piuttosto che nel modo in cui esso è formulato: quasi tutti i problemi possono essere un valido punto di partenza per avventurarsi nel mondo della matematica.
3. Da un lavoro fatto a scuola
SIMMETRIA – LIVELLO 1
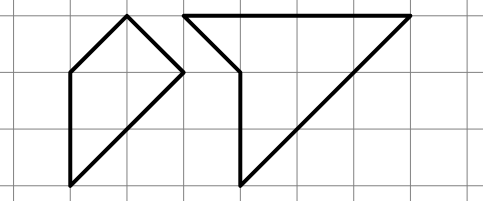
1. Copiate (o fotocopiate) i due poligoni seguenti su un foglio di cartoncino.
2. Poi cercate di unirli in modo da formare un poligono che abbia un asse di simmetria.
3. Infine inventate voi stessi un puzzle simile a questo, formato da due o tre pezzi.

Possibili momenti dell’esplorazione.
- I due pezzi si possono sovrapporre? (no)
- Uno o entrambi i pezzi si possono ribaltare? (non sono previsti ribaltamenti, ma si può esplorare questa possibilità)
- Abbiamo trovato una soluzione, ma come possiamo dimostrare che la figura ottenuta è simmetrica?
- Abbiamo ottenuto due soluzioni. Sono entrambe accettabili?
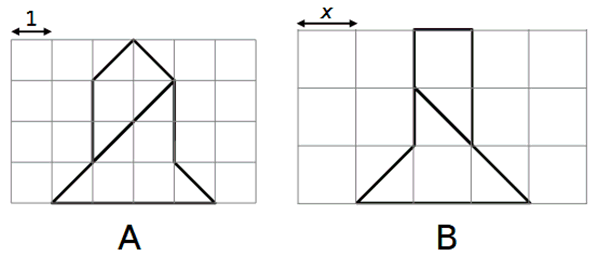
- Se il lato di un quadrato della griglia A è lungo 1, quanto vale x?
- Come si può fare per inventare un nuovo puzzle di questo tipo? (un “trucco” è quello di disegnare prima una figura simmetrica e poi dividerla in pezzi)
4. Un puzzle minimalista di Vesa Timonen
l puzzle seguente è una creazione di Vesa Timonen. La figura è una mia ricostruzione basata su un esemplare di legno, perciò potrebbe non essere esattamente uguale al progetto originale.
Vesa Timonen si definisce più o meno così, sul suo profilo LinkedIn (2023):
“Sono un designer di puzzle freelance. Il mio obiettivo è quello di progettare puzzle che diano alle persone momenti di “a-ha”, insegnino il pensiero logico ed esercitino resistenza e grinta.”
SIMMETRIA – LIVELLO 2
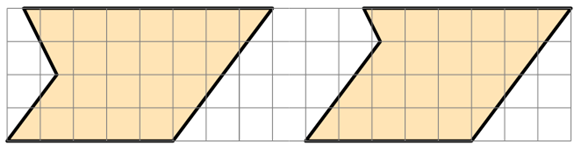
- Copiate (o fotocopiate) il puzzle seguente su un cartoncino e ritagliate i due pezzi.
- Cercate di unire i due pezzi in modo da ottenere una figura simmetrica.
Possibili momenti dell’esplorazione.
- Dopo aver risolto il puzzle, confrontatelo con quello precedente e descrivete le difficoltà che avete incontrato.
- Se provate a rifarlo dopo qualche giorno, ci riuscite facilmente o incontrate le stesse difficolta?
5. Un puzzle di Tadao Kitazawa
L’esempio seguente è ispirato a una proposta di Tadao Kitazawa e può essere utile per scoprire la simmetria rotazionale. Nella richiesta infatti non si specifica che la simmetria debba essere solo assiale. Una delle tre soluzioni non ha un asse di simmetria ma un centro di simmetria. (Tadao Kitazawa, 2021, modificato)
SIMMETRIA – LIVELLO 3
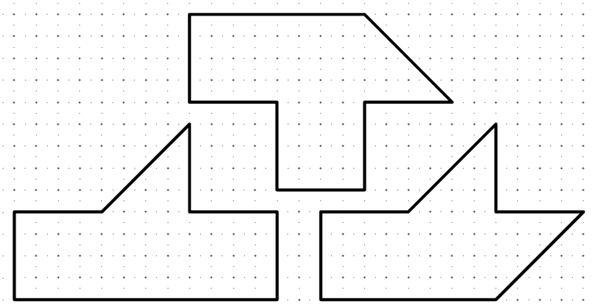
1. Copiate (o fotocopiate) il puzzle seguente su un cartoncino e ritagliate i tre pezzi.
2. Mettete assieme i tre pezzi in modo da ottenere una figura simmetrica.
3. Il puzzle ha tre soluzioni: chi è capace di trovarle?
In una soluzione i pezzi vanno solo ruotati, nelle altre invece un pezzo va ribaltato.
Questa esplorazione ci aiuta a comprendere temi legati alla ricerca matematica contemporanea, per esempio Erik Demaine e altri autori, nell’articolo Symmetric assembly puzzles are hard, beyond a few pieces, dimostrano che tale problema è fortemente NP-completo anche se i pezzi sono tutti polimini. (Erik Demaine e altri, 2020).
Illustrazioni: Gianfranco Bo
Foto cover: peampath2812 / Shutterstock

