Risolvere le equazioni con il metodo di Lagrange
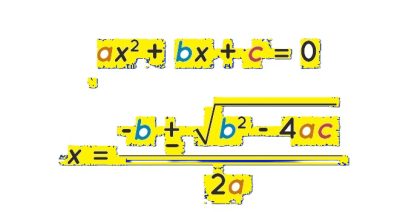
La formula risolutiva dell’equazione di secondo grado ottenuta con il metodo di Lagrange. Relazioni fra coefficienti e radici.
«Il miglior maestro è quello che pensi meno a comparir lui, e lasci fare i giovani, dissimulando la sua opera e creando in loro questa illusione che quello che imparano sono loro stessi che l’hanno trovato». Francesco De Sanctis
Un’espressione spesso abusata è “Le vie del Signore sono infinite“. Ne vale però la pena: aiuta a non far perdere la speranza. Prima o poi un premio per chi lavora ci sarà sempre. Come per Margherita, la giovane dottoranda protagonista del film il Teorema di Margherita: alla fine la sua “ossessione” è premiata! Una soluzione, anche se parziale, al problema che l’ha presa in spirito e mente, riesce a trovarla. Un modo per dire che anche le vie della matematica sono infinite e un problema, prima o poi, lo diceva anche David Hilbert, si riesce sempre a risolvere. E questo vale anche nell’insegnamento: alla fine i docenti bravi riescono ad avere il loro premio e a sentirsi gratificati da allievi e ambiente di lavoro.
Il docente bravo non è apatico, è sempre entusiasta di quello che insegna, lo spiega con passione e sa spiegarlo in tanti modi diversi, sa seguire più vie per chiarire e legare fra loro concetti e idee della matematica. In ogni caso non s’addormenta sul proprio sapere per usare la bella espressione che Francesco De Sanctis, ministro, pronunciò nel suo discorso al Parlamento.
Consideriamo l’equazione:
ax2+bx + c =
Continua la lettura su: https://www.matmedia.it/risolvere-le-equazioni-con-il-metodo-di-lagrange/ Autore del post: Matmedia Fonte: http://www.matmedia.it
