Warning: Constant WP_POST_REVISIONS already defined in /home/mhd-01/www.maestravera.it/htdocs/wp-config.php on line 82Warning: Constant DISALLOW_FILE_EDIT already defined in /home/mhd-01/www.maestravera.it/htdocs/wp-config.php on line 82maestravera.ithttps://www.maestravera.it
Materiale didattico per la scuola primariaSat, 18 Mar 2023 11:31:19 +0000it-IT
hourly
1 https://wordpress.org/?v=6.1.7https://www.maestravera.it/wp-content/uploads/2019/04/cropped-MaestraVera-32×32.jpegmaestravera.ithttps://www.maestravera.it
3232Sistemi o Apparati? Differenza e classificazionehttps://www.maestravera.it/sistemi-apparati-corpo-umano/
Mon, 21 Sep 2020 15:43:15 +0000https://www.maestravera.it/?p=624Spesso parliamo di sistemi e di apparati come se fossero sinonimi, invece c’è una differenza tra i due termini che è bene chiarire presto ai ragazzi prima di iniziare ad affrontare i vari sistemi e apparati che formano il corpo umano. Ogni essere vivente è costituito da semplici unità viventi chiamate cellule. Gli organismi pluricellulari, […]L’articolo Sistemi o Apparati? Differenza e classificazione proviene da maestravera.it.
]] >
Spesso parliamo di sistemi e di apparati come se fossero sinonimi, invece c’è una differenza tra i due termini che è bene chiarire presto ai ragazzi prima di iniziare ad affrontare i vari sistemi e apparati che formano il corpo umano.
Ogni essere vivente è costituito da semplici unità viventi chiamate cellule. Gli organismi pluricellulari, come l’uomo, sono formati da cellule specializzate ovvero da cellule che svolgono una specifica funzione.
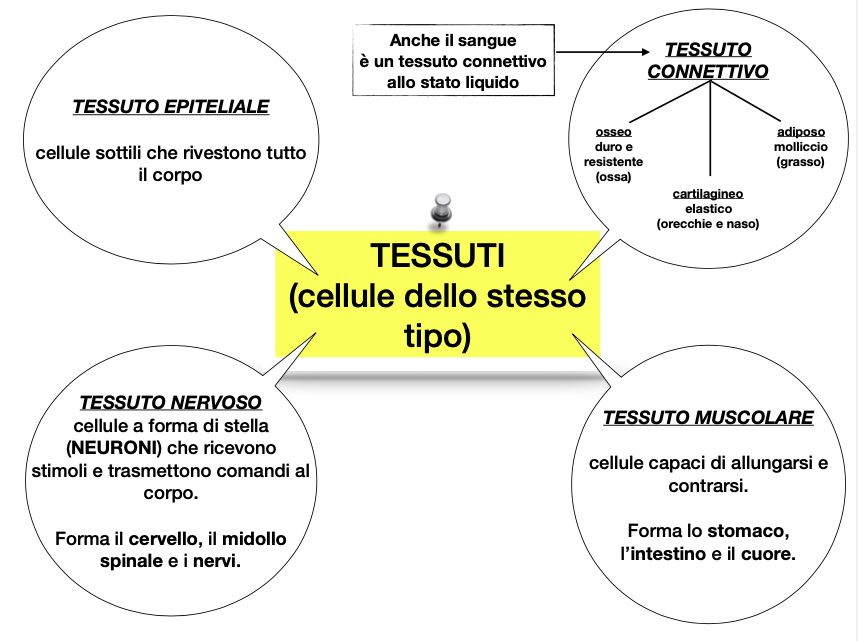
In quarta avevamo già affrontato la cellula animale e vegetale, pertanto abbiamo potuto ripassarla e fare il passo successivo, ovvero chiarire che più cellule dello stesso tipo si uniscono e insieme formano i tessuti.
Nel corpo umano incontriamo varie tipologie di tessuti:
muscolareepitelialeosseonervoso…Per facilitare l’acquisizione della classificazione dei tessuti umani, ho fornito ai ragazzi questo schema riassuntivo.
Schema sui tessuti umaniIl passo successivo è stato comprendere che il corpo umano non è però fatto solo da tessuti e per i ragazzi è stato abbastanza evidente rispondere che è composto da ORGANI. Ne hanno citati molti.
A questo punto ho spiegato che i tessuti che si uniscono per svolgere una funzione specifica formano un organo:
cervellocuorestomaco…Compreso il meccanismo degli incastri, hanno intuito che nella distinzione tra apparato e sistema dovevano necessariamente essere coinvolti gli organi.
Hanno riflettuto sugli apparati che conoscono e li hanno cercati sul libro di testo, semplicemente sfogliando le pagine.
A questo punto è risultato evidente che più organi che contribuiscono a svolgere una funzione più complessa formano un apparato o un sistema, ma qual è la differenza?
La differenza è molto semplice:
Organi diversi che collaborano per uno scopo comune (è il caso dello stomaco e dell’intestino nell’apparato digerente), costituiscono un APPARATO.
Organi simili (come quelli del sistema nervoso), formati cioè da tessuti dello stesso tipo, costituiscono un SISTEMA.
Compresa la differenza tra APPARATI e SISTEMI li abbiamo classificati:
Sistemi
Sono sistemi:
Il sistema scheletrico: formato da cartilagini, ossa e articolazioni.Il sistema muscolare: costituito da muscoli volontari e involontari.Il sistema nervoso: formato da cellule chiamate NEURONIApparati
Sono apparati:
L’apparato digerente: formato da numerosi organi e alcune ghiandole.L’apparato respiratorio: formato dalle vie aeree superiori e inferiori.L’apparato circolatorio: costituito da cuore , vasi sanguigni e vasi linfatici.L’apparato escretore: costituito da reni e vie urinarie.L’apparato tegumentario: costituito da pelle , peli, capelli, unghie, ghiandole sudoripare e sebacee.L’apparato riproduttore: differente tra maschio e femmina.Sul quaderno abbiamo registrato la differenza tra sistemi e apparati e abbiamo iniziato a conoscere quali sistemi e apparati costituiscono il corpo umano.
Per ciascuno abbiamo fatto una piccola rappresentazione. Di seguito riporto un’immagine di riferimento.
Sistemi e ApparatiSe avete bisogno di uno schema chiaro per gli alunni DSA, vi suggerisco di visualizzare quello di Mappe per la Scuola.
L’articolo Sistemi o Apparati? Differenza e classificazione proviene da maestravera.it.
]] >Frazioni proprie, improprie apparenti, equivalentihttps://www.maestravera.it/frazioni-proprie-improprie-apparenti-equivalenti/
Wed, 18 Mar 2020 21:27:33 +0000https://www.maestravera.it/?p=538Lezione di matematica sulle frazioni proprie, improprie, apparenti, complementari e equivalenti. Definizioni, videolezione, schede e appunti.
L’articolo Frazioni proprie, improprie apparenti, equivalenti proviene da maestravera.it.
]] >Per fare un veloce ripasso delle frazioni per la mia quinta ho realizzato un video che riassume i concetti di frazione:
Propria e impropriaComplementareEquivalenteApparentePer rivedere il concetto di frazione, unità frazionaria e intero in questa pagina trovate dei materiali.
Ecco il video:
[embedded content]
Trovo che i mattoncini Lego siano stupendi per rappresentare le frazioni.
La conoscenza per i bambini passa attraverso le mani e maneggiare concretamente i concetti permette loro di interiorizzarli molto più facilmente. I mattoncini oltretutto piacciono molto ai ragazzi, per questo ho chiesto ai ragazzi di esercitarsi nel rappresentare le frazioni utilizzando le frazioni. In questo modo:
Frazione propria:
Indica UNA PARTE dell’intero.
Il numeratore è minore del denominatore e maggiore di ZERO.
Frazione impropria
Indica una quantità maggiore di un intero.
Il numeratore è maggiore del denominatore, ma non è un suo multiplo.
Frazione apparente
Indicano una quantità pari o multipla dell’intero.
Hanno il numeratore uguale o multiplo del denominatore.
QUi un’esercitazione sulle frazioni proprie, improprie e apparenti.
Frazioni equivalenti
Moltiplicando o dividendo il numeratore e il denominatore per lo stesso numero, si ottiene una frazione equivalente alla frazione data.
Per farlo si deve DIVIDERE il numeratore e il DENOMINATORE per un divisore comune.
2/6
Le frazioni equivalenti ci permettono di introdurre anche la semplificazione della frazione, poiché semplificare una frazione significa trasformarla in un’altra equivalente ma con termini minori.
la semplifico:
2 : 2 = 1
6 : 2 = 3
1/3
Frazioni complementari
Qui una scheda sulle frazioni complementari.
L’articolo Frazioni proprie, improprie apparenti, equivalenti proviene da maestravera.it.
]] >Frazioni: termini e unità frazionariahttps://www.maestravera.it/termini-frazione-unita-frazionaria/
Wed, 18 Mar 2020 16:00:36 +0000https://www.maestravera.it/?p=522Lezione di matematica per la scuola primaria sulle frazioni: concetto di frazione, intero, termini della frazione e unità frazionaria. Spiegazione e schede
L’articolo Frazioni: termini e unità frazionaria proviene da maestravera.it.
]] >Il primo passo nel mondo delle frazioni riguarda l’acquisizione chiara del concetto di INTERO e del suo CONTRARIO (non intero), prerequisito fondamentale per la comprensione dei termini della frazione e dell’unità frazionaria.
Un’attività molto semplice che non prevede preparazioni complesse è la piegatura di alcuni fogli di carta, vanno benissimo anche fogli di riciclo.
Si prende un foglio e lo si piega prima in due parti, poi in quattro, poi in otto, poi in sedici parti…
Si ragiona con i bambini sul fatto che il foglio costituisce un intero, perché è un foglio, ma lo abbiamo diviso in 2 parti UGUALI, o in 4 parti UGUALI, o in 8 e così via…
Io ho proposto anche piegature non uguali per permettere di capire la differenza tra la frazione e la non frazione.
Abbiamo raggruppato i fogli divisi in parti uguali in una scatola e i fogli divisi in parti diverse tra loro li abbiamo messi in un’altra scatola.
A questo punto ho introdotto la definizione di frazione ed ho spiegato che:
Parliamo di FRAZIONE quando un intero (un oggetto o una figura) è diviso in parti perfettamente uguali, infatti, quelle parti se sovrapposte coincidono.
Ora che abbiamo compreso in cosa consiste una frazione abbiamo attaccato sulla scatola dei fogli frazionati il cartellino FRAZIONI, mentre sull’altra scatola abbiamo scritto NON FRAZIONI.
Ciascuno ha poi piegato un foglio a proprio piacimento e lo ha riposto in un sacchetto. A turno i bambini hanno pescato dal sacchetto un foglio piegato e lo hanno riposto nella scatola adatta, a seconda che fosse o NON fosse una frazione.
Al termine di questa attività è stato possibile introdurre il termine “frazionare“, che significa dividere in parti uguali e non semplicemente dividere.
Unità Frazionaria e termini della frazione
Il passo successivo è avvicinare i bambini al concetto di unità frazionaria e ai termini della frazione.
Riprendiamo i nostri fogli divisi in parti uguali e per ciascun “pezzettino” comprendiamo quanto vale.
Conoscere e fare proprio il linguaggio delle frazioni è molto importante. Nella vita di tutti i giorni ai bambini sarà capitato di sentir parlare di “una bottiglia da tre quarti”, di “un quarto d’ora”, di “un terzo di strada”, ecc.
I bambini potranno capire che quelle espressioni si riferiscono a qualcosa di concreto e ne comprenderanno il significato.
Dobbiamo spiegare ai bambini che le frazioni si scrivono in un modo un po’ speciale. Le vedranno scritte come due numeri separati da una linea. Un numero sopra, una linea e un altro numero sotto, ovvero il numeratore che indica quante parti uguali consideriamo, mentre il denominatore indica in quante parti uguali è stato diviso il nostro intero.
Per spiegare meglio i termini della frazione e l’unità frazionaria, abbiamo rappresentato sul quaderno il Tricolore. Abbiamo disegnato un rettangolo diviso in 3 parti uguali e abbiamo colorato le singole parti con i colori della bandiera italiana e su ciascuna parte abbiamo scritto la frazione corrispondente:
È importante indicare ai bambini che ciascuna parte si può leggere UN TERZO o UNO FRATTO TRE, poiché la linea di frazione si legge fratto ed esprime una divisione.
È importante sottolineare che ciascuna parte dell’intero frazionato si chiama unità frazionaria.
A questo punto abbiamo provato ad utilizzare la terminologia specifica riflettendo sui colori della bandiera,che rappresentano le singole parti, mentre la bandiera corrisponde all’INTERO:
La parte VERDE corrisponde a UN TERZO della bandiera (intero).La parte BIANCA corrisponde a UN TERZO della bandiera (intero).La parte ROSSA corrisponde a UN TERZO della bandiera (intero).Il passo successivo è stato sommare le singole parti:
La parte verde e la parte bianca INSIEME costituiscono i DUE TERZI della bandiera.La parte rossa e la parte bianca INSIEME costituiscono i DUE TERZI della bandiera…Alla fine abbiamo concluso che tutte le parti colorate rappresentano TUTTA la bandiera, cioè l’INTERO.
Sul quaderno abbiamo registrato i termini della frazione in questo modo:
Per rinforzare l’acquisizione della terminologia ho proposto questa scheda Gianni e le frazioni tratta dalla guida di Gaia Edizioni “Laboratorio di matematica per lo sviluppo, il recupero e il potenziamento degli apprendimenti – II livello”.
Un’attività che piace molto ai bambini, che possono fare a casa come come compito, ma anche a scuola, per imparare in modo divertente, consiste nel rappresentare le frazioni con i mattoncini lego. Potranno manipolare i pezzetti, assemblarli per comporre un intero, frazionarli nelle singole parti, trovare, più avanti, frazioni equivalenti, complementari…
Potete proporre una frazione e chiedere loro di rappresentarla con i mattoncini, in questo modo:
L’articolo Frazioni: termini e unità frazionaria proviene da maestravera.it.
]] >Compito di realtà in cucinahttps://www.maestravera.it/compito-di-realta-equivalenze/
Mon, 16 Mar 2020 21:46:26 +0000https://www.maestravera.it/?p=509Compito di realtà per la classe quinta della scuola primaria: ricetta con quantità da trasformare in grammi e calcolo di quantità.
L’articolo Compito di realtà in cucina proviene da maestravera.it.
]] >Equivalenze
In questi giorni di didattica a distanza stiamo ripassando le equivalenze e per mantenere viva l’attenzione ho pensato di proporre un compito di realtà alla mia classe quinta.
Ho dato ai ragazzi della mia quinta una ricetta per preparare 12 muffin ed ho chiesto loro di:
eseguire le equivalenze per trasformare tutti gli ingredienti in grammifare i calcoli per ricavare gli ingredienti necessari per preparare 7, 26, 45 e 2 muffin.Per i calcoli più difficili ho consentito l’uso della calcolatrice.
Ingredienti, equivalenze e calcoli devono essere trascritti sul quaderno.
Terminata la parte matematica ho chiesto ai ragazzi di scegliere quanti muffin preparare, di munirsi di bilancia e grembiule e preparare i muffin. Se fossimo stati a scuola me ne sarei fatta portare uno il giorno successivo. Siamo a casa e mi accontento di una foto.
Ecco la ricetta. QUI trovate il pdf da dare ai ragazzi.
INGREDIENTI
cacao amaro in polvere 70 g
zucchero 3 hg
latte intero a temperatura ambiente 0,18 kg
bicarbonato 0,02 hg
farina 3000 dg
burro a temperatura ambiente 15000 cg
uova a temperatura ambiente 0,220 kg
lievito in polvere 0,6 dag
PROCEDIMENTO
(TESTO REGOLATIVO)
Per preparare i muffin al cioccolato cominciate versando nella tazza della planetaria il burro a pomata (cioè molto morbido) e lo zucchero. Azionate la frusta e lasciate mescolare per qualche minuto, fin quando non sarà diventato una crema morbida. Se non avete la planetaria potrete utilizzare le fruste elettriche oppure quella a mano. Poi unite le uova a temperatura ambiente e leggermente sbattute un po’ alla volta.
In questo modo il composto si amalgamerà alla perfezione, diventando una massa morbida ed omogenea. Nel frattempo sistemate un setaccio in un recipiente e versate la farina ed il cacao.
Poi il lievito per dolci ed il bicarbonato e setacciate. Un cucchiaio alla volta, inserite le polveri fin quando non saranno completamente assorbite.
L’impasto a questo punto sarà molto consistente quindi allegeritelo aggiungendo il latte a filo, sempre a temperatura ambiente. Sminuzzate il cioccolato al coltello, ottenendo dei pezzettini grandi circa 0,5 mm e aggiungeteli al composto.
Mescolate accuratamente con una spatola per inglobare il tutto e trasferite poi in un sac-à-poche senza bocchetta. Sistemate i pirottini in una leccarda da muffin e spremete circa 100 grammi di impasto così da ottenere 12 tortine.
Cuocete in forno preriscaldato ed in modalità statica a 180° per 28-30 minuti, facendo la prova stecchino per verificarne la cottura (per questi muffin si sconsiglia la cottura in forno ventilato poiché diventerebbero troppo asciutti!). Una volta pronti sfornateli e lasciateli raffreddare o se proprio non resistete, gustate i muffin al cioccolato ancora caldissimi.
(Ricetta di GialloZafferano.it)
“Designed by Tamaratorres / Freepik”I ragazzi si sono divertiti e mi hanno mandato foto incredibili dei muffin. Compito di realtà che la mia classe quinta ha molto apprezzato.
L’articolo Compito di realtà in cucina proviene da maestravera.it.
]] >Sistema Scheletricohttps://www.maestravera.it/sistena-scheletrico/
Mon, 16 Mar 2020 16:26:48 +0000https://www.maestravera.it/?p=496Lezione, sul Sistema Scheletrico, con appunti, metodologia e verifica per la classe quinta della scuola primaria.
L’articolo Sistema Scheletrico proviene da maestravera.it.
]] >Il Sistema Scheletrico è stato il primo sistema che abbiamo affrontato.
Lo abbiamo fatto comprendendo che possiamo parlare di sistema poiché tutti i suoi componenti sono ossa.
Non tutte le ossa del corpo hanno la stessa forma ma tutte quante si somigliano poiché sono formate da cellule dello stesso tipo, pertanto possiamo parlare di SISTEMA SCHELETRICO.
Per prima cosa abbiamo osservato il nostro corpo, ciascuno ha provato a percepire le ossa al tatto e abbiamo provato a nominarle. Partendo dalla faccia abbiamo il cranio, la mascella e la madibola. Abbiamo trovato poi la clavicola e la scapola, le ossa delle braccia, le costole, la colonna vertebrale il bacino e le ossa delle gambe.
Le abbiamo nominate osservando il modellino che abbiamo in classe e facendoci aiutare dall’immagine con la relativa nomenclatura presente sul del libro di testo.
credit: Wikipedia Questo lavoro ci ha permesso di capire che:
TUTTE le ossa presenti nel nostro corpo formano lo scheletro.Le ossa possono essere raggruppate e distinte in tre gruppi: ossa del CAPOossa del TRONCO ossa degli ARTIFunzioni del Sistema Scheletrico
Abbiamo poi riflettuto sulle funzioni del sistema scheletrico, partendo da una domanda molto banale: come saremmo se non avessimo le ossa?
Le risposte sono state molto divertenti e hanno rivelato una grandissima immaginazione. Qualcuno ha ricordato un termine già visto in quarta: INVERTEBRATI e ciò ci ha permesso di capire che senza il sistema scheletrico saremmo degli invertebrati.
Lo scheletro, insieme ai muscoli, è ciò che SOSTIENE il nostro corpo e permette il MOVIMENTO.
Subito dopo, ragionandoci un po’, i ragazzi hanno capito che un’altra importante funzione è quella di proteggere alcuni organi vitali, come CUORE, POLMONI e CERVELLO.
Abbiamo così individuato le principali funzioni del sistema scheletrico:
SOSTEGNO del corpoMOVIMENTO (insieme ai muscoli)PROTEZIONE degli organi vitaliAbbiamo aggiunto che il Sistema Scheletrico ha anche le importanti funzioni di:
– PRODURRE cellule del sangue, grazie al midollo spinale che scorre nella colonna vertebrale.
– RISERVA di sali minerali, poiché le ossa sono formate anche da sali minerali.
Questa precisazione ci ha permesso di passare alla seconda domanda:
Da cosa sono formate le ossa?
Struttura delle ossaSul quaderno abbiamo provato a rappresentare la struttura delle ossa, nominando le varie parti.
Ci siamo soffermati, in particolare, sugli OSTEOBLASTI, la cui funzione è stata oggetto di numerose curiosità, perché abbiamo scoperto che permettono l’accrescimento delle ossa.
Gli osteoblasti ricostituiscono continuamente il tessuto osseo, mentre gli osteoclasti lo distruggono. O meglio, rimuovono continuamente il tessuto più vecchio. Quindi il tessuto osseo “più usato” viene rimosso dagli osteoclasti e sostituito da tessuto nuovo di zecca prodotto dagli osteoblasti.
A livello delle estremità delle ossa lunghe (epifisi) è presente, nella fase di crescita dell’individuo, un particolare tipo di cartilagine, chiamata cartilagine di accrescimento che verrà poi sostituita da tessuto osseo. Le ossa, infatti, non restano sempre della stessa dimensione ma crescono con noi.
Lo scheletro di un adulto è formato da 206 ossa ed esse sono formate da acqua, sali minerali e osseina.
A questo punto abbiamo preso delle ossa di pollo e un contenitore contenente dell’aceto. Abbiamo immerso le ossa nell’aceto e le abbiamo lasciate per qualche giorno.
Esperimento osseinaSuggerisco di utilizzare un contenitore con coperchio se non volete avere la classe pervasa dall’odore dell’aceto.
Questa esperienza ci ha permesso di osservare attentamente le ossa e ha stimolato la curiosità dei ragazzi.
Ci ha dato modo di comprendere che le ossa sono sono formate da qualcosa che le rende dure e da qualcosa che le rende morbide.
Prima di immergere le ossa nell’aceto abbiamo provato a spezzarle, senza riuscirci.
Dopo il trattamento con l’aceto siamo riusciti a piegarle e a spezzarle potendo così osservare il tessuto spugnoso.
Abbiamo pertanto dedotto, visto che l’aceto ha sciolto i sali minerali, che l’osseina rende le ossa elastiche ( quel qualcosa di morbido a cui prima non avevamo saputo dare un nome), mentre i sali minerali le rendono dure.
Abbiamo registrato sul quaderno quanto appreso, dopodiché abbiamo creato uno scheletro grandezza naturale, che ci accompagnerà nel viaggio alla scoperta del corpo umano e verrà arricchito, di volta in volta dei vari organi e tessuti.
Lo scheletro murale da stampare ed assemblare lo trovate QUI.
Le ossa e le articolazioni
Comprese le funzioni del Sistema Scheletrico, la composizione delle ossa e la suddivisione delle ossa del corpo, abbiamo operato un’ulteriore classificazione delle ossa distinguendole in:
ossa LUNGHE: ossa degli artiossa CORTE: vertebre, ossa delle mani…ossa PIATTE: ossa del cranio, del bacino…Abbiamo poi compreso che le ossa solo tra loro collegate e unite.
Sono collegate tra loro dalle articolazioni che possono essere mobili (come quelle del ginocchio o delle spalle che ci permettono movimenti ampi), semimobili (come le aricolazioni vertebrali che permettono movimenti limitati) o fisse (è il caso delle articolazioni del cranio, le quali non consentono alcun movimento).
Articolazioni e legamentiHo poi spiegato ai ragazzi che le ossa sono unite tra loro da fasci di fibre chiamati LEGAMENTI e ovviamente dai muscoli, i quali rivestono le ossa e contribuiscono a tenerle unite.
Per concludere ho fornito ai ragazzi lo schema riassuntivo di Mappe per la Scuola ed ho chiesto loro di articolare un discorso sul sistema scheletrico, spiegando:
Cos’è il Sistema Scheletrico?Quali sono le funzioni del Sistema Scheletrico?Da cosa è formato?Come sono formate le ossa?Che caratteristiche danno alle ossa l’osseina e i sali minerali?Come possono essere classificate le ossa dello scheletro e che funzioni anno?Cosa sono le articolazioni? Come possono essere?Verifica
QUI potete trovare la verifica sul sistema scheletrico.
L’articolo Sistema Scheletrico proviene da maestravera.it.
]] >Il Sistema Solarehttps://www.maestravera.it/il-sistema-solare/
Sun, 15 Mar 2020 23:12:44 +0000https://www.maestravera.it/?p=461Lezione sul sistema solare pensata per la classe quinta della scuola primaria Completa di video, schede, metodologia e spiegazioni sul sistema solare.
L’articolo Il Sistema Solare proviene da maestravera.it.
]] >Il Sistema Solare è uno dei miei argomenti preferiti del programma di quinta ed è sempre apprezzatissimo anche dai ragazzi. L’universo ha da sempre affascinato gli uomini e le donne di tutti i tempi e vale anche per i nostri ragazzi moderni.
Qualche anno fa con una quinta abbiamo scelto di partecipare all’evento di BergamoScienza e per quell’occasione abbiamo realizzato un laboratorio che ci è piaciuto molto e ci ha dato un sacco di soddisfazioni.
Questa esperienza mi ha permesso di produrre e raccogliere un bel po’ di materiale sul Sistema Solare. Ne raccolgo qui una parte che ho conservato.
Presentazione del Sistema Solare
Per introdurre l’argomento ai ragazzi, ho scritto una storia che vi allego. L’ho intitolata “Con il cielo negli occhi”. Mi piace sempre iniziare nuovi argomenti con dei testi o dei libri e in questo caso scrivere questo breve racconto è stato piacevole anche per me. La trovate QUI!
Per prima cosa ho fornito ai ragazzi una scheda informativa sul Sistema Solare, la potete trovare QUI che hanno letto a gruppi, quindi individualmente sul quaderno hanno lavorato con questa scheda (Scheda sul Sistema Solare).
Abbiamo visto il video di “Paxi e il Sistema Solare” realizzato dall’ESA. Ne trovate anche altri molto belli sul sito ESAkids (ha una sezione dedicata alla didattica).
[embedded content]
Carta d’identità dei pianeti
Quindi ho diviso la classe in 8 gruppi e ciascun gruppo ha approfondito un pianeta ed ha raccolto le informazioni per realizzare la carta d’identità di ciascun pianeta. Le informazioni sono state registrate sia sul quaderno sia su un cartellone.
La carta d’identità del pianeta ha lo scopo di:
Evidenziare gli aspetti ritenuti più importanti per ciascun pianeta Fornire gli indizi fondamentali per poter poi costruire i modelli tridimensionali dei pianeti Abbiamo pertanto inserito:
”DIMENSIONI” e “DISTANZE ” dei pianeti – per riflettere sul concetto che lo spazio è vuoto, ovvero che le dimensioni dei pianeti sono trascurabili rispetto alle distanze che li separano.“COLORE” e “SUPERFICIE” – per poter ricavare le caratteristiche chimiche e fisiche che serviranno per la scelta dei materiali utili alla costruzione dei pianeti.“TEMPERATURA” – perché dal confronto tra i pianeti si dedurrà che la temperatura dipende: dalla vicinanza o lontananza dal Sole dall’ esposizione verso il Sole,dalla presenza o assenza dell’atmosfera.“ATMOSFERA”, le informazioni trovate ci faranno scoprire che può essere:uno scudo protettivo dalle radiazioni solari e dagli asteroidimolto densa a causa dei gas che la compongonoquasi inesistente per la troppa vicinanza al Sole (forte campo gravitazionale).“SATELLITI”, la presenza o l’assenza e la quantità di satelliti che ruotano intorno ad un pianeta, sono dovute alla forza d’attrazione gravitazionale del pianeta stesso e alla sua posizione rispetto al Sole.“CURIOSITA’”, spazio libero per qualsiasi approfondimento.
Carta d’Identità dei PianetiRiduzione in scala dei Pianeti
Un’attività che ha unito scienze e matematica è la riduzione in scala delle dimensioni dei pianeti e delle distanze.
Osservare le dimensioni dei pianeti e della loro distanza dal sole, ci ha permesso di imparare i grandi numeri. Abbiamo visto che l’astronomia è uno di quei campi dove i grandi numeri sono impiegati spessissimo.
Per ridurre i pianeti e le loro distanze abbiamo dovuto utilizzare due scale differenti. In matematica ne abbiamo approfittato per parlare dell’approssimazione e dell’arrotondamento, poiché chiaramente le nostre riduzioni in scala non sono perfette ma approssimative e arrotondate. Devo dire che questo lavoro molto concreto ha aiutato i ragazzi a comprendere il concetto senza troppa fatica.
Grazie a questa riduzione abbiamo realizzato questa riproduzione:
Pianeti in scala realisticaAnche il questo caso ci siamo agganciati alla matematica ed abbiamo affrontato la circonferenza. Per realizzare il cartamodello del sole abbiamo costruito un compasso con gesso e spago. Abbiamo quindi compreso che la circonferenza è 3 volte e un po’ il diametro.
Sul quaderno ci siamo esercitati con il compasso e abbiamo disegnato i pianeti:
Mercurio con un diametro di 0,5 cm, Venere 1,2 cm, la Terra 1,3 cm, Marte 0,7cm, Giove 14 cm, Saturno 12 cm, Urano e Nettuno 5 cm. Prima i ragazzi hanno dovuto calcolare il raggio per aprire il compasso alla giusta ampiezza.
Per la riduzione in scala delle distanze tra i pianeti abbiamo utilizzato una scala differente:
Una volta completi tutti i calcoli ci siamo muniti di un rotolo di carta, di un metro e di cartelli con i nomi dei pianeti e, dopo aver misurato e misurato, abbiamo osservato le distanze dei pianeti.
Ci siamo resi conto che i pianeti terrestri sono molto vicini tra di loro, mentre i pianeti gioviani sono molto distanti sia rispetto al Sole, sia tra di loro. Abbiamo anche osservato che tra Marte e Giove c’è uno spazio molto grande ed abbiamo ipotizzato che lì potesse anche starci un pianeta, infatti, documentandoci abbiamo scoperto che gli scienziati credono che la cintura asteroidale sia un pianeta che non è riuscito a formarsi. Probabilmente a causa delle forze contrapposte esercitate dal Sole e da Giove.
Riproduzione dei pianeti
I ragazzi, nei rispettivi gruppi, hanno realizzato i pianeti. La scala per la riproduzione dei pianeti l’ho fornita io:
RIPRODUZIONE DEI PIANETI IN SCALAChi sceglierà di cimentarsi in questa attività non potrà esimersi dal ricercare informazioni in merito a COLORE” e “SUPERFICIE”, per poter ricavare le caratteristiche chimiche e fisiche che serviranno per la scelta dei materiali per la realizzazione del modellino.
A questo punto direi che se
Diametri dei pianeti (1 m = 139.640 Km) per avere una scala coerente
Pianeti e diametri in cm per i modellini
Mercurio 3.5 cm
Venere 8.5 cm
Terra 9 cm
Marte 5 cm
Giove 100 cm
Saturno 83 cm
Urano 36 cm
Nettuno 35 cm
Per i Pianeti terrestri consiglio materiali duri, che richiamino la natura rocciosa di tali corpi.
Materiali suggeriti:
– palline di polistirolo di 3,5; 5; 9 centimetri
– cartapesta per il rivestimento esterno.
Per Giove, come per gli altri Pianeti giganti, suggerisco materiali morbidi per riflettere la natura gassosa di questi corpi.
Materiali suggeriti:
palloni o simili del diametro di 95, 80 e 30 centimetri circaovatta sintetica per il rivestimento esterno.Per la coloritura i pianeti rocciosi possono essere colorati con le tempere, mentre quelli gassosi devono essere colorati con le bombolette.
Abbiamo riprodotto il Sistema Solare in diversi modi, anche utilizzando il cibo… ed è stato molto divertente!
Sistema Solare in cucinaIn questo video potete vedere un riassunto del lavoro fatto.
[embedded content]
Per concludere abbiamo parlato dei movimenti della Terra attorno al Sole e su se stessa.
Rotazione e rivoluzione dei pianeti
I ragazzi si sono avvicinati ai concetti di rotazione e di rivoluzione attraverso delle esperienze pratiche. Nel cortile della scuola abbiamo tracciato le orbite dei pianeti e i ragazzi prendendo il posto dei pianeti hanno rivoluzionato attorno al sole, rendendosi in questo modo conto che i pianeti gassosi, essendo più lontani hanno molta più strada da percorrere per fare un giro completo intorno al sole, mentre i pianeti terrestri hanno un’orbita molto più piccola, pertanto hanno meno strada da fare per compiere una rivoluzione completa attorno al sole.
Questa attività ci ha permesso di comprendere il motivo dell’alternarsi del giorno e della notte (rotazione) e delle stagioni (rivoluzione). Per chiarire meglio le idee ai ragazzi, ho fornito loro questa scheda sugli equinozi:
La luna e le fasi lunari
Come ultimo capitolo del Sistema Solare, abbiamo affrontato la Luna, il satellite della Terra.
Abbiamo visto il video di Paxi sulla Luna:
[embedded content]
Abbiamo costruito la “Scatola della luna” con una scatola delle scarpe. Qui potete trovare le istruzioni. Il risultato è davvero incredibile: sembra davvero di avere la luna in una scatola. Qualcuno l’ha realizzata anche a casa.
Abbiamo osservato le fasi lunari anche infilzando con un bastoncino di legno una palla di polistirolo e abbiamo osservato l’ombra del sole su di essa mentre simulavamo una rivoluzione attorno alla Terra.
Abbiamo quindi registrato sul quaderno che la Luna è il satellite della Terra, non ha luce propria, non ha atmosfera, non ha acqua se non sotto forma di ghiaccio ai poli.
Si è formata, probabilmente dalla collisione di un giovane pianeta con la Terra e da questa collisioni ha avuto origine la Luna.
Abbiamo registrato le fasi lunari sul quaderno con questa scheda:
Scheda per registrare le fasi lunari. Le alette, dopo aver tagliato il contorno, si piegano e sulla parte non disegnata si scrive il nome della fase solare corrispondente.Abbiamo anche registrato che la Luna compie tre movimenti:
attorno alla Terra – RIVOLUZIONEsu se stessa – ROTAZIONEattorno al Sole insieme alla Terra – TRASLAZIONEAllego un pdf sul Sole e sulla Luna che abbiamo letto in classe. Lo potete trovare QUI.
Questo laboratorio è stato caratterizzato dal divertimento pertanto non poteva mancare una riproduzione delle fasi lunari utilizzando i biscotti.
In questo video vedete le fasi lunari realizzate da me, ma lo abbiamo fatto anche in classe. I ragazzi hanno apprezzato molto.
[embedded content]
Per concludere allego una scheda di approfondimento e un glossario sul Sistema Solare.
Verifica
QUI una verifica sul Sistema Solare.
L’articolo Il Sistema Solare proviene da maestravera.it.
]] >Apparato Tegumentariohttps://www.maestravera.it/apparato-tegumentario/
Sat, 14 Mar 2020 16:46:19 +0000https://www.maestravera.it/?p=445Lezione di scienze, sull’apparato tegumentario, per la classe quinta della scuola primaria. Appunti e schede per una spiegazione completa.
L’articolo Apparato Tegumentario proviene da maestravera.it.
]] >Come primo argomento del corpo umano, dopo aver affrontato la cellula e la differenza tra tessuti, apparati e sistemi, ho scelto di affrontare la pelle perché è il rivestimento del corpo, la sua custodia. Una sorta di coperta che protegge i tessuti e gli organi che costituiscono il corpo umano.
Prendendo spunto dal libro della Erikson “Scienze facili per la classe quinta”, siamo partiti dall’analisi della parola TEGUMENTO.
I ragazzi non conoscevano il significato di questo termine, pertanto abbiamo ricercato la definizione, che riporto:
tegumento /tegu’mento/ s. m. [dal lat. tegumentum “copertura”]. – (biol.) [rivestimento di un intero organismo, animale o vegetale] ≈ epidermide, Ⓖ pelle, [di organismo vegetale] corteccia, [di organismo vegetale] scorza.Abbiamo così arricchito il nostro vocabolario con una parola nuova, che d’ora in poi utilizzeremo in modo corretto.
A questo punto siamo passati all’osservazione della pelle e alla scoperta degli elementi che la costituiscono.
I ragazzi hanno facilmente individuato i protagonisti dell’apparato tegumentario:
pellepeliunghiecapelliRagionandoci ancora un po’ hanno intuito che mancava ancora qualcosa:
ghiandole sebacee ghiandole sudoripareAbbiamo quindi capito che la pelle è il tessuto che riveste tutto il corpo umano e costituisce l’apparato tegumentario. È l’organo più esteso del corpo umano.
Ha diverse funzioni, tra cui proteggere il corpo, regolarne la temperatura e percepire stimoli termici, dolorifici e pressori (tattili).
La pelle è composta da più strati:
l’epidermide è lo strato esterno protettivo ed è costituita da più strati; il derma permette di percepire il calore e il dolore ed è ricco di vasi sanguigni; l’ipoderma è ricco di grasso corporeo e ha una funzione di isolamento, poiché funge da cuscinetto protettivo per i muscoli.Per semplificare il recupero delle informazioni abbiamo registrato sul quaderno quanto è emerso dalla conversazione .
Ecco gli appunti:
Quindi ho fornito loro questa scheda che ho preparato:
Per approfondire ulteriormente possiamo dare qualche informazione sugli strati dell’epidermide.
Gli strati dell’epidermide
Lo strato corneo è lo strato più superficiale dell’epidermide, è chiamato cute, ed è costituito da molti strati di cellule appiattite e disposte su più strati. Si possono considerare due porzioni: una più profonda e compatta in cui le cellule (corneociti) sono unite tra loro, ed uno superficiale in cui le cellule (dette squame cornee) tendono a staccarsi per desquamazione. La pelle è, infatti, un organo estremamente dinamico, poiché le sue cellule si rinnovano continuamente. Più sotto abbiamo lo strato lucido, che si trova solo nella cute spessa (palmo della mano e pianta dei piedi).Lo stato granuloso è l’ultimo strato di cellule vive.Lo stato spinoso è uno strato spesso, formato da cellule chiamate cheratinociti, che risalgono gradualmente verso la superficie.Lo strato basale è lo strato più profondo dell’epidermide ed è sostenuto da una membrana basale che lo separa dal derma sottostante.Per consolidare questi concetti, abbiamo costruito un supporto visivo utilizzando un modellino di carta della pelle. Per farlo abbiamo utilizzato questo modello trovato in rete:
Qui potete scaricare la versione in bianco e nero.
Curiosità: Perché la pelle degli uomini ha colori differenti?
Nel mondo il colore della pelle umana si distribuisce su una tavolozza dalle dalle molte sfumature e per arrivarci sono servite decine di migliaia di anni. Anche se il colore della pelle è diverso non sono diversi gli antenati. Abbiamo tutti la stessa origine evolutiva.La pelle più scura è vantaggiosa per chi vive nelle regioni molto soleggiate, come quelle attorno all’equatore, mentre quella più chiara è vantaggiosa per chi abita nelle regioni più fredde, meno esposte al sole e più vicine ai poli.Diversi milioni di anni fa, questa distinzione però non esisteva, perché gli ominidi come l’Australopiteco Lucy avevano la pelle ricoperta da peli molto estesi e non erano molto diversi dagli scimpanzé.
Quando l’uomo iniziò a cacciare assumendo un’andatura eretta, si spinse negli spazi aperti e soleggiati della savana. Questo fece in modo che si liberasse dei peli in eccesso. Ciò facilitò la sudorazione e la dispersione del calore.
Se l’intensità dei raggi che ci investono è determinata dalla posizione geografica in cui viviamo, la quantità di raggi che penetra nell’organismo dipende dalla concentrazione di melanina.La melanina è un pigmento marrone scuro che è presente in maggiori quantità nella pelle di chi vive a latitudini tropicali, perché protegge la pelle dai raggi solari, impedendo scottature.
Con il tempo, l’uomo si spostò verso nord e verso sud, muovendosi dall’equatore verso località più vicine ai poli. Ai poli il problema principale non era più contrastare i raggi UV dannosi, ma produrre abbastanza vitamina D, indispensabile per la salute delle ossa, nonostante la poca esposizione solare: bisognava permettere che una certa quantità di raggi solari fosse assorbita dalla pelle (e quindi, occorreva meno melanina, che è un “filtro solare” naturale). Nelle regioni più settentrionali, la pelle è perciò divenuta più chiara.
Grazie a questi meccanismi, diverse popolazioni, a diverse latitudini e in diversi momenti storici hanno sviluppato diversi colori della pelle. Una differenza solo superficiale e nata dalle stesse, universali esigenze di adattamento.
Tratto da: “FocusJunior.it > Scienza > Curiosità scientifiche > Perché abbiamo il colore della pelle diverso?”
Per concludere l’argomento ho fornito lo schema preso dal sito mappe per la scuola ed ho chiesto ai ragazzi di formulare un discorso di qualche minuto sull’apparato tegumentario. Per facilitare il compito ho assegnato alcune “domande guida” per permettere loro di focalizzare i punti salienti da evidenziare:
Cosa significa tegumento?Da quali elementi è costituito l’apparato tegumentario?Quali sono le funzioni della pelle?Da quali strati è costituita la pelle? Quali funzioni svolgono?Queste domande possono essere poi proposte come interrogazione scritta.
L’articolo Apparato Tegumentario proviene da maestravera.it.
]] >Apparato Circolatoriohttps://www.maestravera.it/apparato-circolatorio/
Sat, 14 Mar 2020 13:57:22 +0000https://www.maestravera.it/?p=421Lezione di scienze per la classe quinta della scuola primaria sull’apparato circolatorio
L’articolo Apparato Circolatorio proviene da maestravera.it.
]] >Ho dovuto affrontare l’apparato circolatorio nella mia classe quinta della scuola primaria, nel periodo di sospensione delle attività didattiche, quindi lo abbiamo trattato a distanza per l’emergenza coronavirus.
In classe lo avevamo solo introdotto e non volevo che continuassero a studiarlo solo dal libro, per questo ho preparato una videolezione per arrivare agli alunni nel modo più efficace nonostante la distanza.
L’articolo Apparato Circolatorio proviene da maestravera.it.
]] >“Uno” di Isabella Pagliahttps://www.maestravera.it/letture-per-la-classe-prima-primaria-uno-di-isabella-paglia/
Thu, 18 Apr 2019 20:36:06 +0000https://www.maestravera.it/?p=398“Uno” è un libro per bambini di classe prima, scritto da Isabella Paglia e illustrato da Andrea Scoppetta. Lettura pensata per lettori alle prime armi, è scritto interamente in maiuscolo, presenta numerosi spunti di riflessione perché porta all’attenzione di grandi e piccini il tema della diversità, dell’accettazione dell’altro e del rispetto. Il protagonista è un […]
L’articolo “Uno” di Isabella Paglia proviene da maestravera.it.
]] >“Uno” è un libro per bambini di classe prima, scritto da Isabella Paglia e illustrato da Andrea Scoppetta.
Lettura pensata per lettori alle prime armi, è scritto interamente in maiuscolo, presenta numerosi spunti di riflessione perché porta all’attenzione di grandi e piccini il tema della diversità, dell’accettazione dell’altro e del rispetto.
Il protagonista è un simpatico extraterrestre la cui astronave atterra sulla Terra a causa di un guasto.
Unico sopravvissuto della sua specie, Uno inizia a vivere sulla Terra ma immergersi nella società, giocare coi bambini, farsi accettare, gli risulta estremamente complicato e resta solo per così tanto tempo che non ricorda più il suo vero nome e finisce per chiamare se stesso “Uno”.
Uno veste con abiti sgargianti e fa grossi sorrisi di tutti i colori, senza però riuscire a fare amicizia, così ogni giorno torna alla sua astronave tutto solo.
Una notte un’altra astronave atterra vicino alla sua e una creatura bizzarra, che dice di chiamarsi “Qualcuno”, bussa alla sua porta chiedendo aiuto.
“Qualcuno” è molto diverso da “Uno” e inizialmente lui ne è spaventato, perciò non lo fa entrare, ma dopo qualche esitazione ripensa al freddo che sente dentro ogni volta che lo evitano ed accoglie Qualcuno nella sua casa.
Da quel momento inizia una bella amicizia tra Uno e Qualcuno, un’amicizia stravagante, colorata, divertente, ma soprattutto contagiosa!
Finalmente anche tutti gli altri comprendono che non è necessario essere uguali per essere amici e nessuno, da quel momento, ha più paura di fare cose diverse.
Isabella Paglia ci presenta la diversità e il cambiamento per quello che è, ovvero un’occasione di crescita e di rinnovamento. La diversità spaventa perché ci costringe a rimetterci in discussione, ma accettare gli altri, accogliendone le diversità come qualcosa di positivo è l’unico mezzo che abbiamo per crescere.
[embedded content]
Lettura consigliatissima!!!
L’articolo “Uno” di Isabella Paglia proviene da maestravera.it.
]] >