Galois fu il primo a usare il termine gruppo
Antologia di belle pagine ad uso dei docenti anche in formazione. L’importanza della teoria dei gruppi in matematica e in fisica. Galois fu il primo a usare il termine gruppo.
Il passo che segue è tratto dall’articolo Gruppi di George W. Mackey (1916 – 2006) dell’Enciclopedia del Novecento dell’Istituto dell’Enciclopedia Italiana fondata da Giovanni Treccani, Vol II (1978)
La grande importanza della teoria dei gruppi in matematica e in fisica è in parte dovuta alle seguenti circostanze. Molti dei sistemi che vengono studiati contengono un grado minore o maggiore di simmetria, nel senso che le relazioni oggetto di studio vengono lasciate invariate da certe trasformazioni biunivoche degli elementi del sistema stesso.
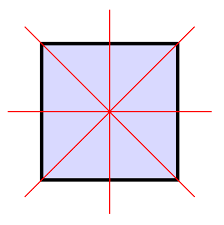
Per esempio, un quadrato nel piano è simmetrico relativamente a rotazioni di multipli interi di 90° intorno al suo centro, a riflessioni rispetto alle diagonali e rispetto alle rette che tagliano per metà due lati opposti. In ogni caso, la famiglia di tutte queste simmetrie costituisce un gruppo di trasformazioni e l’analisi della ‛struttura’ di questo gruppo risulta sovente uno strumento prezioso per la comprensione delle proprietà e della struttura del sistema stesso. Può infatti addirittura accadere che tutte le proprietà di un’entità matematica complessa siano implicite nella struttura del suo gruppo di simmetria.
La potenza di questo metodo di analisi è stata per la prima volta riconosciuta in relazione alla teoria della risoluzione di equazioni algebriche mediante radicali. Nel 1770, G. L. Lagrange pubblicò una lunga memoria, nella quale sottopose a una profonda analisi i metodi conosciuti
Continua la lettura su: https://www.matmedia.it/galois-fu-il-primo-a-usare-il-termine-gruppo/ Autore del post: Matmedia Fonte: http://www.matmedia.it
