Trova l’intruso che non c’è: lo avete risolto?
La settimana scorsa vi ho proposto alcuni esercizi ispirati alle idee di Christopher Danielson, ma senza riprodurne direttamente i contenuti. Potete ritrovare qui il post con tutti gli spunti, ora è venuto il momento di scoprire quali sono le soluzioni. Prima però ripeto di seguito un passaggio importante per rinfrescare lo spirito di questi esercizi.
Nella Matematica, oltre la matematica
Molti pensano che un problema di matematica dovrebbe essere chiaro, preciso, con tutte le informazioni necessarie e solo quelle, e avere una soluzione ben determinata e indiscutibile.
Questo va bene ma certamente non è il punto di partenza per chi vuole imparare a pensare come un matematico. E’ invece un traguardo da conquistare.
Giochi come “Trova l’intruso” sono divertenti e aiutano a sviluppare questo modo di pensare.
Ma se l’intruso non ci fosse? Forse la vera sfida non è trovare la risposta giusta, ma ripensare la domanda, per vedere le cose in modo diverso.
Tu mi chiedi di trovare l’intruso, ma io posso dimostrarti che nessuno lo è perché tutti hanno una proprietà speciale che gli altri non hanno e questa è a sua volta una proprietà di secondo livello che li accomuna, nessuno escluso.
Le nuove idee matematiche emergono da una nuvola, si chiariscono a poco a poco guardandole da vicino attraverso il ripensamento e la discussione.
A volte si rivelano diverse da da come sembravano all’inizio, altre volte rimangono aperte a più interpretazioni.
Questo è il modo in cui si impara la matematica e riflette anche la sua storia: un continuo gioco tra chiarezza e dubbi, regole e sorprese, domande e scoperte.
E ora, ecco le soluzioni!
Risposte & riflessioni
Attenzione! Questi problemi possono avere molte soluzioni.
Quelle che trovate qui sono esempi da discutere e ampliare, senza porre limiti all’inventiva.
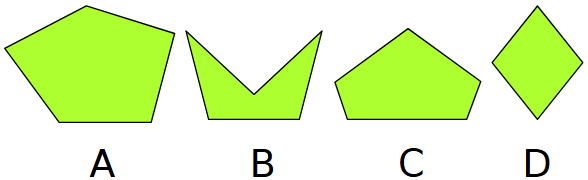
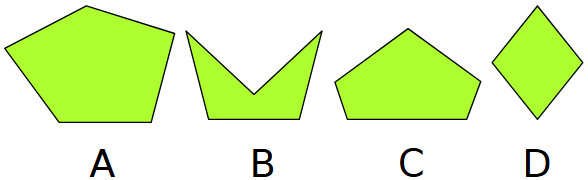
Esercizio 1. Figure piane
Quale forma non c’entra con le altre e perché?
Esamina ogni terna di figure e trova una proprietà che hanno in comune ma che la quarta figura non ha.

Possibile soluzione.
- La A perché non ha un asse di simmetria mentre le altre ne hanno uno.
- La B perché è concava mentre le altre sono convesse.
- La C perché non ha i lati tutti uguali mentre le altre figure li hanno tutti uguali.
- La D perché ha 4 lati mentre le altre hanno 5 lati.
Esercizio 2. Figure piane
Quale forma non c’entra con le altre e perché?
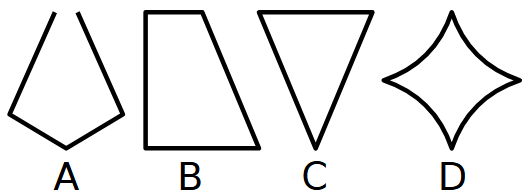
Possibile soluzione.
- La A perché è aperta mentre le altre sono chiuse.
- La B perché non ha un asse di simmetria mentre le altre ne hanno almeno uno.
- La C perché ha 3 lati mentre le altre hanno 4 lati.
- La D perché ha i lati curvi mentre le altre li hanno rettilinei.
Esercizio 3. Numeri
Quale numero non c’entra con gli altri e perché?
Esamina ogni terna di numeri e trova una proprietà che hanno in comune ma che il quarto numero non ha.
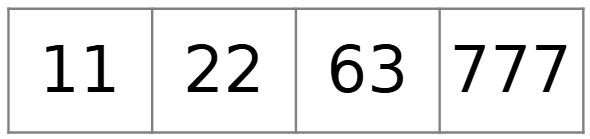
Possibile soluzione.
- l’11 perché è primo mentre gli altri sono composti.
- Il 22 perché è pari mentre gli altri sono dispari.
- Il 63 perché è non è multiplo di 11 mentre tutti gli altri lo sono.
- Il 777 perché ha 3 cifre mentre gli altri ne hanno 2.
Esercizio 4. Numeri
Quale numero non c’entra con gli altri e perché?

Possibile soluzione.
- l’1 perché ha 1 cifra mentre gli altri ne hanno 2.
- Il 25 perché è un quadrato perfetto mentre gli altri sono cubi.
- Il 27 perché è un cubo perfetto mentre gli altri sono quadrati.
- Il 64 perché è pari mentre gli altri sono dispari.
Esercizio 5. Questa volta l’intruso c’è.
Quale forma non c’entra con le altre e perché?
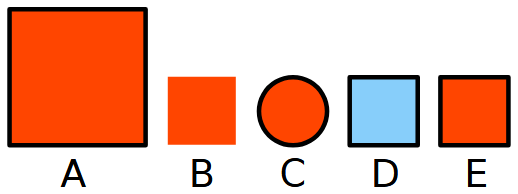
- La A è grande mentre tutte le altre sono piccole.
- La B è non ha il contorno mentre tutte le altre lo hanno.
- La C è un cerchio mentre tutte le altre sono quadrati.
- La D è blu mentre tutte le altre sono rosse.
- La forma E, in cosa si distingue da TUTTE le altre? E’ un quadrato, piccolo, rosso col contorno ma non è l’UNICA ad avere ciascuna di queste caratteristiche.
E qui arriva il ragionamento filosofico: la E è l’unica a NON avere qualcosa di speciale e proprio questo la rende diversa da tutte le altre!
Quindi la forma che non c’entra è la E.
Ma forse questa soluzione è contraddittoria…
Esercizio 6. Numeri e fantasia
Quale numero non c’entra con gli altri e perché?
Puoi usare anche proprietà non strettamente matematiche!

Possibile soluzione.
- Il 4 perché è capovolto mentre gli altri sono dritti.
- Il 7 perché è primo mentre gli altri sono composti.
- Il 18 perché è rosso mentre gli altri sono neri.
- Il 69 perché è l’unico che se viene ruotato di 180° rimane un numero uguale a se stesso.
Pace e bene a tutti.
GfBo
Foto cover: Senorina_Irina / Shutterstock
Ilustrazioni: Gianfranco Bo
L’articolo è pubblicato anche su BASE Cinque.