Numeri sul cubo: lo avete risolto?

Nell’ultimo post abbiamo esplorato quanto affrontare un problema matematico possa diventare un’esperienza potente quando ti consente di esplorare la tua rete di conoscenze personali. Di diventarne consapevole. Di espanderla. Pubblichiamo qui le risposte.
Problema 1. Numeri sui vertici di un cubo
Assegna un numero da 0 a 7, senza ripetizioni, a ciascun vertice di un cubo in modo tale che la somma degli estremi di ogni spigolo sia un numero primo.

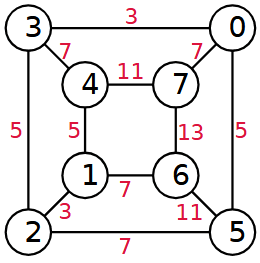
Altre domande sul problema 1
- Quante soluzioni diverse ha questo problema, a meno di rotazioni del cubo?
- Come posso trovare tutte le soluzioni scrivendo un programma per computer?
- Se risolvo questo problema con l’Intelligenza artificiale, cosa posso imparare di nuovo per me?
Per le prime due domande i lavori sono ancora in corso…
Cosa ho imparato dall’A.I. su questo problema
Per la terza domanda, segnalo una cosa carina, che mi ha sorpreso.
Il sistema di A.I. Perplexity in versione freemium, come tanti altri, è basato sul testo e non sulle immagini. Perciò deve trovare un modo “testuale” di rappresentare e “vedere” il cubo come grafo.
Ebbene, ha associato ciascuno degli 8 vertici del cubo a numero binario di 3 bit, come illustrato qui sotto. I tre bit sono le coordinate 3D dei vertici di un cubo di spigolo lungo 1.
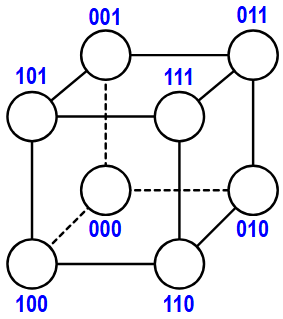
A (000)
B (001)
C (010)
D (011)
E (100)
F (101)
G (110)
H (111)
Come identifica le coppie di vertici connessi da uno spigolo?
Usa questa proprietà: Due vertici del cubo sono connessi da uno spigolo se e solo se i loro numeri binari differiscono esattamente in una sola cifra.
In altre parole, due vertici sono connessi quando la distanza di Hammig dei loro codici binari è 1.
Forte, vero?
Problema 2. Facce costanti
Etichetta i vertici di un cubo con i numeri 1, 2, 3, 4, 5, 6, 7, 8 senza ripetizioni, in modo che la somma dei numeri ai quattro vertici di ciascuna faccia sia costante.
Ecco, per esempio, una delle 6 soluzioni possibili.
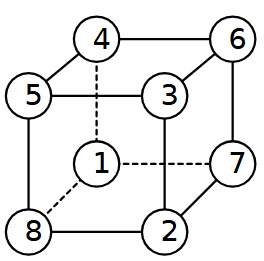
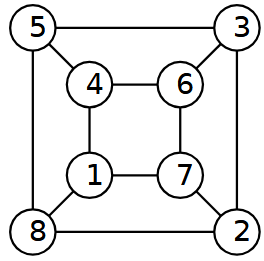
Problema 2. Facce costanti
- Quale deve essere l’unica somma possibile dei numeri su ciascuna faccia del cubo?
Risposta: 18 - Quante soluzioni distinte ha il problema, a meno di rotazioni del cubo?
Risposta: 6
Foto cover: Boryana Manzurova / Shutterstock
Ilustrazioni: Gianfranco Bo
L’articolo è pubblicato anche su BASE Cinque.