La media aritmetica come punto di minimo
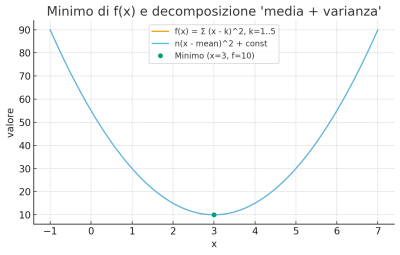
Un quesito di dieci anni fa: il minimo di una funzione quadratica. Dalla derivata alla statistica: è la media aritmetica il punto di minimo
Nel 2015, alla sessione ordinaria della maturità scientifica, fu proposto il seguente quesito:
Sia ( f ) la funzione, definita per tutti gli ( x ) reali, da
[
f(x)=(x-1)^2+(x-2)^2+(x-3)^2+(x-4)^2+(x-5)^2.
] Determinare il minimo di ( f ).
La via diretta
La derivata prima è
[
f'(x)=2big[(x-1)+(x-2)+(x-3)+(x-4)+(x-5)big]=10x-30,
] da cui ( f'(x)=0 iff x=3 ).
Essendo ( f”(x)=10>0 ), si ha che il minimo cade in ( x=3 ).
Il valore corrispondente è
[
f(3)=(-2)^2+(-1)^2+0^2+1^2+2^2=10.
]
Perché proprio la media?
In generale, per numeri reali fissati ( a_1,dots,a_n ):
[
f(x)=sum_{i=1}^n (x-a_i)^2
] raggiunge il minimo quando ( x ) è la media aritmetica dei punti ( a_i ).
Sviluppando,
[
f(x)=n x^2 – 2!left(sum_{i=1}^n a_iright)x + sum_{i=1}^n a_i^2,
] si riconosce una parabola con vertice in
[
x=frac{sum_{i=1}^n a_i}{n}.
]
Quattro vie alternative 1) Completamento del quadrato (media + varianza)
Introduciamo la media:
[
bar a=frac{1}{n}sum_{i=1}^n a_i.
]
Per ogni termine,
[
x-a_i=(x-bar a)+(bar a-a_i).
]
Allora
[
(x-a_i)^2 = (x-bar a)^2 + 2(x-bar a)(bar a-a_i) + (bar a-a_i)^2.
]
Sommando su tutti gli indici:
[
sum_{i=1}^n (x-a_i)^2 = sum (x-bar a)^2 + 2(x-bar a)sum(bar a-a_i) + sum (bar a-a_i)^2.
]
(sum (x-bar a)^2 = n(x-bar a)^2) perché è la stessa quantità ripetuta (n) volte. (sum(bar a-a_i)=nbar a-sum a_i=0) per definizione di media.
Quindi rimane:
[
sum_{i=1}^n (x-a_i)^2 = n(x-bar a)^2 + sum_{i=1}^n (bar a-a_i)^2.
]
Il secondo termine è costante (non dipende da (x)), mentre il primo è minimo per (x=bar a).
Così si giustifica perché la funzione
Continua la lettura su: https://www.matmedia.it/la-media-aritmetica-come-punto-di-minimo/ Autore del post: Matmedia Fonte: http://www.matmedia.it
