Ancora un quesito di maturità
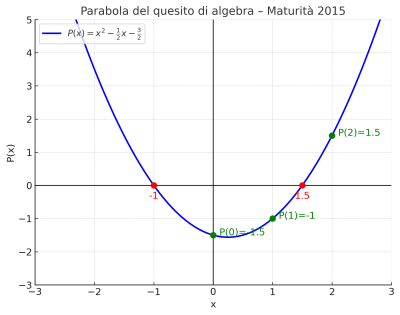
Un quesito di algebra della maturità 2015 formulato nel linguaggio delle funzioni. Un esercizio semplice ma ricco di spunti didattici, affrontato in più modi.
Nella storia della seconda prova scritta della maturità scientifica, il 2015 rappresenta un momento di passaggio importante: è il primo anno in cui le Indicazioni Nazionali entrano a pieno regime. Le tracce di quell’anno riflettono bene questa fase singolare: da un lato introducono elementi di “novità”, dall’altro mantengono, in misura preponderante, lo stile e i contenuti del percorso avviato nel 2001 con la nuova struttura della prova articolata in problemi e quesiti.
In precedenti articoli, elaborati insieme a ChatGPT, abbiamo già analizzato due dei quesiti della sessione 2015 quali esempi di continuità con l’impianto di quel quindicennio di innovazioni che aveva caratterizzato la seconda prova.
Il primo è un problema storico di massimizzazione, proposto nel 1547 da Ludovico Ferrari a Niccolò Tartaglia:
“Si divida il numero 8 in due numeri reali non negativi in modo che sia massimo il prodotto di uno per l’altro e per la loro differenza”.
Un quesito antico ma sorprendentemente attuale, che abbiamo affrontato in più modi per evidenziarne il valore didattico.
Il secondo riguarda lo studio di una funzione quadratica, definita da
[
f(x)=(x-1)^2+(x-2)^2+(x-3)^2+(x-4)^2+(x-5)^2,
]
per la quale occorreva determinare il minimo. Anche in questo caso, la ricchezza delle strategie risolutive ha messo in luce l’efficacia di quesiti densi di significato matematico.
Adesso ne affrontiamo un terzo, forse il più semplice ma non per questo meno interessante dal punto di vista didattico specie se si
Continua la lettura su: https://www.matmedia.it/ancora-un-quesito-di-maturita/ Autore del post: Matmedia Fonte: http://www.matmedia.it
