Maturità scientifica 2025 – Sessione straordinaria. Le risposte ai quesiti 1–4 della prova di Matematica dell’11 settembre
Di seguito pubblichiamo le soluzioni ai primi quattro quesiti della traccia della sessione straordinaria.
Quesito 1
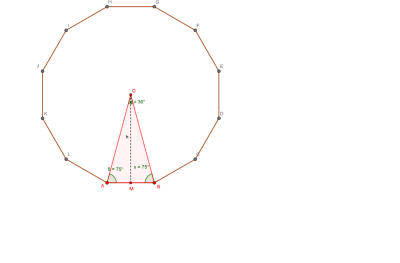
Determinare il perimetro e l’area di un poligono regolare di lato 4 cm, sapendo che gli angoli interni sono ampi 150°.
Soluzione
Il numero (n) dei lati del poligono si ricava dalla relazione (nalpha=(n-2)pi), dove (alpha) è l’ampiezza di ciascun angolo interno:[n=frac{2pi}{pi-alpha}]
Essendo (alpha=tfrac{5}{6}pi), si ha[n=frac{2pi}{pi-frac{5}{6}pi}=frac{2pi}{frac{pi}{6}}=12]
Il poligono è un dodecagono regolare di lato (4,text{cm}); pertanto, la misura del perimetro è (48,text{cm}).
L’ampiezza dell’angolo al centro è (tfrac{pi}{6}). Per calcolare il valore dell’area, determiniamo la misura del segmento (OM), apotema del poligono e altezza del triangolo isoscele di base (AB).Gli angoli alla base del triangolo (ABO) hanno ampiezza (tfrac{5}{12}pi). Pertanto,[overline{OM}=overline{AM},tan!left(tfrac{5}{12}piright)=overline{AM},(2+sqrt{3})]
Infatti[tanfrac{alpha}{2}=frac{sinalpha}{1+cosalpha}=frac{sinleft(tfrac{5}{6}piright)}{1+cosleft(tfrac{5}{6}piright)}=frac{tfrac{1}{2}}{1-tfrac{sqrt{3}}{2}}=frac{1}{2-sqrt{3}}=frac{2+sqrt{3}}{4-3}=2+sqrt{3}]
Con (AM=tfrac{s}{2}=2) e (P=48), l’area risulta[A=frac{Pcdot a}{2}=frac{48cdotbigl(2(2+sqrt{3})bigr)}{2}=24,(4+2sqrt{3})=96+48sqrt{3} text{cm}^2approx 179{,}14 text{cm}^2]
Quesito 2
Un’urna contiene 16 palline numerate da 1 a 16. Vengono estratte in blocco 5 palline dall’urna; qual è la probabilità che il numero più grande tra quelli usciti sia maggiore di 9?
Soluzione
Il numero di cinquine che si possono ottenere estraendo in blocco 5 palline in un gruppo di 16 corrisponde al numero di combinazioni di classe 5 di 16 oggetti:[binom{16}{5}=frac{16cdot 15cdot 14cdot 13cdot 12}{5!}=4368]
Il numero delle cinquine che contengono almeno un numero maggiore di 9 è complementare del numero di cinquine che contengono solo numeri (le 9). Calcoliamo, pertanto, la probabilità dell’evento[A: {text{la cinquina estratta è costituita da numeri compresi tra 1 e 9, estremi inclusi}}]
[mathbb{P}(A)=frac{binom{9}{5}}{binom{16}{5}}=frac{126}{4368}=frac{3}{104}]
L’evento complementare è[B=overline{A}: {text{la cinquina estratta contiene almeno un numero maggiore di 9}},]
[mathbb{P}(B)=1-frac{3}{104}=frac{101}{104}approx 0{,}9712]
Metodo diretto
Suddividiamo idealmente l’insieme delle 16 palline in due gruppi: il gruppo (A) costituito dalle 7 palline corrispondenti ai numeri > 9 e il gruppo (B) costituito dalle 9 palline contrassegnate con numeri (le 9).Il gruppo delle 5 palline estratte conterrà (binom{7}{k}) palline provenienti dal gruppo (A) e (binom{9}{5-k}) provenienti dal gruppo (B); quindi, la scelta può avvenire in (binom{7}{k}cdot binom{9}{5-k}) modi diversi.
k
C1 = (binom{7}{k})
C2 = (binom{9}{5-k})
C1·C2
P(A)
P(B)
0
1
126
126
0,0288
0,9712
1
7
126
882
2
21
84
1764
3
35
36
1260
4
35
9
315
5
21
1
21
Totale
4368
4242
All’evento (A) corrisponde solo la prima riga (tutte (le 9)); all’evento (B) l’unione delle rimanenti. La distribuzione dei valori del prodotto (binom{7}{k}cdot binom{9}{5-k}), in funzione di (k), spiega il risultato (mathbb{P}(B) > mathbb{P}(A)).
Quesito 3
Quanti sono i numeri naturali di tre cifre tali che la cifra “8” compare almeno una volta? Quanti quelli in cui la cifra “0” compare almeno una volta?
Soluzione
I numeri di 3 cifre sono in tutto (9cdot 10^2=900) (la prima cifra non può essere 0).
Quelli che non contengono la cifra 8 sono (8cdot 9^2=648); quelli che la contengono almeno una volta sono[9cdot 10^2-8cdot 9^2=900-648=mathbf{252}]
Quelli che non contengono la cifra 0 sono (9^3=729); quelli che la contengono almeno una volta sono[9cdot 10^2-9^3=900-729=mathbf{171}]
Quesito 4
Mostrare che, nello spazio tridimensionale, il piano di equazione (x+2y-3z-7=0) è tangente alla superficie sferica (S) di equazione (x^2+y^2+z^2-2x+2y-4z-8=0) e stabilire le coordinate del punto di tangenza (T). Scrivere, inoltre, l’equazione di una retta che sia tangente alla superficie (S) nel punto (T).
Soluzione
Un piano è tangente a una sfera se e solo se la sua distanza dal centro è uguale al raggio della sfera.La superficie sferica (S) ha il centro nel punto (C(1,-1,2)) e raggio di lunghezza[r=sqrt{1+1+4+8}=sqrt{14}]
La retta (n) passante per (C) e perpendicolare al piano (pi: x+2y-3z-7=0), di vettore normale ((1,2,-3)), ha equazioni parametriche[n: begin{cases}x=1+t\y=-1+2t\z=2-3tend{cases}]
Il punto (P) di intersezione di (n) con (pi) corrisponde al valore di (t) che soddisfa[1+t+2(-1+2t)-3(2-3t)-7=0 Rightarrow t=1.]
Pertanto (P=(2,1,-1)). Poiché (overline{PC}=sqrt{14}=r), il piano (pi) è tangente alla sfera (S) e (P) coincide con (T), punto di tangenza.
Una qualsiasi retta passante per (T) e giacente sul piano (pi) è tangente alla superficie sferica (S) e può essere determinata come intersezione di (pi) con un piano del fascio avente come sostegno la retta (n).Dalle equazioni parametriche di (n) si possono individuare due piani (alpha) e (beta) che la contengono:[begin{cases}t=x-1\[2pt]
t=dfrac{y+1}{2}\[6pt]
t=dfrac{2-z}{3}end{cases} Rightarrowr: begin{cases}x-1=dfrac{y+1}{2}\[6pt]
x-1=dfrac{2-z}{3}end{cases} Rightarrow\begin{cases}2x-y-3=0\3x+z-5=0end{cases}]
Il fascio di piani passanti per (n) è dato da[2x-y-3+k(3x+z-5)=0 Rightarrow (2+3k)x – y + kz -3-5k=0.]
Le infinite rette giacenti su (pi) e tangenti in (T) alla sfera sono individuate dal sistema[begin{cases}(2+3k)x – y + kz -3-5k=0\x+2y-3z-7=0end{cases}]
Una retta particolare si ottiene imponendo, al piano del fascio, il passaggio per il punto d’intersezione di (pi) con l’asse (y): (Qleft(0,tfrac{7}{2},0right)).Sostituendo si ottiene (-tfrac{7}{2}-3-5k=0 Rightarrow k=-tfrac{13}{10}), e quindi[begin{cases}19x+10y+13z-35=0\x+2y-3z-7=0end{cases}]
Trascurando il caso generale, la retta (r) può essere determinata anche come retta congiungente i due punti (T) e (Q):[frac{x-2}{-2}=frac{y-1}{tfrac{5}{2}}=frac{z+1}{1}qquad (text{retta } r).]
I due sistemi rappresentano la stessa retta, passante per (T) e (Q), vista come intersezione di coppie di piani diversi.