Una curiosità matematica rimasta tale per due secoli

Matmedia 28/11/2025

Dalla soluzione dell’equazione (x^x = a) alla storia della trasformata W di Lambert: una trasformazione rimasta nascosta per due secoli.

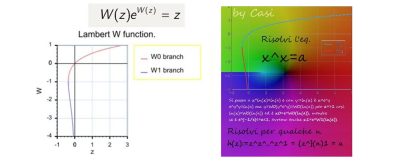
Il problema di risolvere l’equazione trascendente (x^x = a) è un classico che non può essere risolto con le funzioni elementari, come logaritmi o potenze semplici. Si risolve ricorrendo a una funzione speciale, capace di agire come una trasformazione che rende il problema risolvibile. Questa funzione è la Funzione W di Lambert (o funzione Omega). Ecco i passaggi della trasformazione per isolare la x.

La Trasformazione (Funzione W di Lambert)

La Funzione W di Lambert, definita (W(z)), è data come funzione inversa della funzione (f(w) = w·e^w). In altre parole, se: (z = w·e^w) allora, per definizione, si ha (w= W(z)). L’obiettivo della trasformazione è portare l’equazione (x^x = a) nella forma (w·e^w = z).

Applicazione per passi elementari all’Equazione (x^x = a)

Passo A: Applicare il Logaritmo Naturale
Partiamo dall’equazione data: (x^x = a)
Applichiamo il logaritmo naturale ln a entrambi i membri: (ln(x^x) = ln(a))
Per la proprietà dei logaritmi (ln(b^c) = c·ln(b)), otteniamo: (x·ln(x) = ln(a))

Passo B: Trasformare x in un Esponenziale
Dobbiamo far comparire la base e per sfruttare la definizione della Funzione W.
Sappiamo che (x) può essere sempre scritto come (e^{ln(x)}).
Sostituiamo x con (e^{ln(x)}) nel primo membro: (e^{ln(x)}·ln(x) = ln(a))

Passo C: Applicare la Funzione W
L’equazione è ora nella forma desiderata (w·e^w = z), dove: (w = ln(x)) e (z = ln(a)). Applicando la Funzione W di Lambert a entrambi i membri (in modo tale da invertire l’espressione

Continua la lettura su: https://www.matmedia.it/una-curiosita-matematica-rimasta-tale-per-due-secoli/ Autore del post: Matmedia Fonte: http://www.matmedia.it

Categorie: Matmedia, Vedi tutti i blog di Didattica

Tags: Donald E. Knuth, E. M. Wright, Enciclopedia Matematica, Insegnamento, Lambert, leonardo eulero, logaritmo, Trasformata Z

Matmedia

utente matmedia

Emergenza Coronavirus COVID-19: notizie e provvedimenti

Ordinanza del 2 giugno 2021 Ulteriori misure urgenti in materia di contenimento e gestione dell’emergenza epidemiologica da COVID-19.

Ordinanza 29 maggio 2021 Ai fini del contenimento della diffusione del virus Sars-Cov-2, le attività economiche e sociali devono svolgersi nel rispetto delle “Linee guida per la ripresa delle attività economiche e sociali”, elaborate dalla Conferenza delle Regioni e delle Provincie autonome, come definitivamente integrate e approvate dal Comitato tecnico scientifico, che costituiscono parte integrante della presente ordinanza

Ordinanza 21 maggio 2021 Protocollo condiviso di aggiornamento delle misure per il contrasto e il contenimento della diffusione del virus SARS-Cov-2/COVID-19 negli ambienti di lavoro.

Ordinanza 21 maggio 2021 Linee guida per la gestione in sicurezza di attivita’ educative non formali e informali, e ricreative, volte al benessere dei minori durante l’emergenza COVID-19.

Ordinanza 21 maggio 2021 Ulteriori misure urgenti in materia di contenimento e gestione dell’emergenza epidemiologica da COVID-19.

FLC CGIL Scuola 10/01/2022

Quoziente di potenze con la stessa base: spiegazione e definizione

Le potenze, argomento di cui abbiamo avuto modo di discutere negli articoli precedenti nel nostro blog, sono uno degli strumenti matematici fondamentali che ci permettono di manipolare numeri in modo più efficiente. Quando affrontiamo espressioni con potenze che hanno la stessa base, una delle operazioni più comuni che possiamo ritrovare, oltre al prodotto di potenze con la stessa base, è il quoziente tra due potenze, concetto di cui ne esploreremo regole e proprietà all’interno del nostro articolo.

Quoziente di potenze: definizione

Il quoziente fra due potenze aventi stessa base e diverso esponente è uguale a una potenza che ha per base la stessa base e per esponente la differenza degli esponenti. In termini matematici: na : nb = na-b. n

Questa nozione, quindi, spiega come, qualora bisognasse calcolare il quoziente di potenze con la stessa base, sia necessario riportare la stessa base presente in entrambe le potenze, e porre come esponente, la differenza degli esponenti appartenenti alle due potenze da calcolare. Al fine di semplificare è possibile riportare alcuni esempi come:

25:23= 25-3= 22= 4

104:102= 104-2= 102= 100

Inoltre, qualora ci ritrovassimo di fronte ad un quoziente di potenze per la stessa potenza, come nel seguente caso am:a0= am-0= am, il risultato equivale sempre ad 1. Situazione opposta nel quoziente di potenze con esponente zero, come am:a0= am-0= am, dove il risultato equivale sempre alla potenze originale, ossia am.

Applicazioni in problematiche realistiche

Il quoziente di potenze con la stessa base trova applicazioni in vari contesti della vita reale, come nelle scienze, nell’ingegneria e nell’economia. Ad esempio, nella crescita esponenziale di una popolazione o nel decadimento radioattivo, le regole dei quozienti di potenze sono essenziali per modellare e comprendere tali fenomeni.

Nel corso del nostro articolo, quindi, abbiamo ampliato il concetto delle potenze illustrando la regola del quoziente di potenze con la stessa base, evidenziando la sua importanza e fornendo esempi pratici. Comprendere queste regole è fondamentale per affrontare problemi matematici più complessi e applicarli in contesti del mondo reale. La matematica delle potenze è un elemento chiave nella risoluzione di problemi e nella modellazione di fenomeni naturali, sottolineando l’importanza di acquisire una solida comprensione di queste regole.

Se hai ritenuto interessante il nostro post, ti consiglio di non perdere il successivo, uscente domenica prossima alle ore 7:00 del mattino, che riguarderà la potenza di potenza, un altro importantissimo argomento che contribuisce alla realizzazione dei tanti rami in cui la matematica è in grado di diramarsi.

Blog 10/12/2023

Articoli Correlati