La successione ricorsiva “Guarda e dimmi” di Conway

L’esoterismo di una successione che, dietro una regola linguistica per bambini, rivela legami con Fibonacci e una sorprendente “tavola periodica” di 92 elementi.

Nei precedenti articoli abbiamo considerato di volta in volta ricorsioni sempre più sofisticate, ma sostanzialmente della stessa natura numerica e aritmetica: le funzioni annidate, le “sposate” di Hofstadter, quella auto-descrittiva di Golomb e altre.

Con la successione Guarda e dimmi accade qualcosa di radicalmente diverso: la ricorsione è tutta concentrata a descrivere ciò che si vede. La matematica si intreccia con il linguaggio: il numero non è più valore, ma sequenza di simboli da osservare e descrivere.

In classe, l’insegnante è alla lavagna

Scrive: 111 e chiede: «Che cosa vedete?». Uno studente risponde: «Centoundici».

L’insegnante replica: «Sì, questo ne è il significato. Ma provate non a leggere il numero, ma a dire ciò che vedete. Cosa vedete davvero?».

Un altro alunno: «Tre 1». «Benissimo. Lo scrivo così»: 31.

Nuova domanda: «Cosa vedete ora?». Gli studenti: «Un 3 e un 1».
«Dunque scrivo»: 1311.

E ancora: «Cosa vedete?». Gli studenti: «Un 1, un 3, 2 uno».
«Perfetto. Allora scrivo»: 111321. Che vedo? 31131211.

Riscriviamo in sequenza:

111 → 31 → 1311 → 111321 → 31131211 → …

È questa la successione ricorsiva: guardo, descrivo ciò che vedo, e ripeto meglio nota come successione Look-and-say di John Horton Conway (1937 – 2020), matematico inglese famoso per il “Game of Life” e per la sua straordinaria creatività.

La ricorsione non opera sui numeri come quantità, ma come stringhe di simboli: ogni passo è la descrizione del precedente e possiamo darne una definzione più formale in questo modo: data una stringa di cifre

x₁ x₂ … x_k

il termine successivo si ottiene così:

si legge la stringa da sinistra verso destra;
si raggruppano le cifre uguali consecutive (i run);
per ogni run si scrive: numero delle ripetizioni + cifra ripetuta.

Esempio su 111321:

111 → “tre 1” → 31
3 → “un 3” → 13
21 → “un 2, un 1” → 1211

Combinando tutto si ottiene:

31131211

In definitiva conta solo ciò che si vede: è una ricorsione linguistica, non aritmetica.

Costruire successioni ricorsive “guarda e descrivi” o “guarda e dimmi” è apparso molto facile anche a bambini di quarta primaria: si sono divertiti a costruirne altre usando, anziché le cifre arabiche, le lettere dell’alfabeto.

Ad esempio, con semi A e B:

A → 1A → 111A → 311A → 13211A → 111312211A → 31131122211A → …
B → 1B → 111B → 311B → 13211B → 111312211B → 31131122211B → …

e per il seme AB:

AB → 1A1B → 111A111B → 311A311B → 13211A13211B → …

In questi esempi emergono regolarità sorprendenti: i termini della successione AB, sono dati, passo dopo passo, dalla “somma” (nel senso della concatenazione) delle stringhe generate separatamente da A e da B. I bambini lo hanno notato subito confermando così che fare matematica con la ricorsività “premia” e consente di raggiungere buoni obiettivi di osservazione, classificazione, descrizione.

In ogni caso, un buon rafforzamento della procedura ricorsiva guarda e descrivi passa certamente dalla sua costruzione in contesti diversi dalle cifre arabiche.

Il contesto può essere ad esempio il sistema di numerazione dei Romani

Se il seme è il numerale I, la successione è:

I → II → III → IIII → IVI → IIIVII → IIIIIVIII → …

Oppure può essere il sistema binario: se il seme è 0

0 → 10 → 1110 → 101110 → 1110101110 → …

Questi esempi spingono a indagare per rilevare nella successione regolarità, invarianze, particolarità. Ad esempio: se un seme è formato da un blocco doppio (z = xy), la successione generata da (z) è semplicemente la concatenazione delle successioni generate da (x) e (y)?

Talvolta sì (come per il seme AB di prima), ma non sempre. Siano i semi (x = 3), (y = 2), (z = 32).

Scriviamo i primi termini:

[
begin{aligned}
x &= 3 ;to; 13 ;to; 1113 ;to; 3113 ;to; 132113 \
y &= 2 ;to; 12 ;to; 1112 ;to; 3112 ;to; 132113 \
z &= 32 ;to; 1312 ;to; 11131112 ;to; 31133112 ;to; 1321232112
end{aligned}
]

All’inizio sembra funzionare:

[
32 = 3,2, qquad 1312 = 13,12, qquad 11131112 = 1113,1112.
]

Ma al passo successivo:

– la successione da (x = 3) produce (132113),
– la successione da (y = 2) produce (132113),
– la successione da (z = 32) produce invece:
[
1321232112,
]
che non coincide con
[
132113132113.
]

Dunque, nel caso standard non vale la regola di concatenazione: la successione Look-and-say che parte da (32) non è data dalle successioni che partono da (3) e da (2).

Alla portata anche di alunni del primo ciclo sono un’ampia gamma di domande del tipo: ci può essere “un gruppo di più di tre 2?” e “un gruppo di quattro 1?”. In quali casi è possibile ritrovare tra i termini della successione il gruppo 33 o 44 o 55, o 99? Perchè ogni termine della successione sembra avere una lunghezza pari?

Nell’analisi delle successioni un dato che non sfugge, infatti, è la lunghezza dei suoi termini.

È qui che viene fuori la più meravigliosa delle sorprese della Look and say: un comportamento che appare volerla accomunare alla successione di Fibonacci.

Sono successioni completamente diverse:

nel caso di Fibonacci i termini sono numeri;
nel caso Look-and-say i termini sono stringhe di cifre;

eppure entrambe portano a un “invariante numerico”, a una costante.

La successione di Fibonacci soddisfa:

[
F_{n+1} = F_n + F_{n-1}.
]

I rapporti fra termini consecutivi convergono alla sezione aurea:

[
frac{F_{n+1}}{F_n} to varphi = frac{1+sqrt{5}}{2}.
]

Qui crescono numeri: grandezze aritmetiche.
La crescita è esponenziale. Più precisamente, per (n) grande vale la formula asintotica

( F_n approx dfrac{varphi^n}{sqrt{5}} qquad )

Nella Look-and-say i termini non sono numeri, ma stringhe.
Sia:

[
L_n = text{lunghezza del termine n-esimo}.
]

Per il seme (1) ecco i primi tredici termini

1
11
21
1211
111221
312211
13112221
1113213211
31131211131221
13211311123113112211
11131221133112132113212221
3113112221232112111312211312113211
1321132132111213122112311311222113111221131221

Le lunghezze sono:

[
1,;2,;2,;4,;6,;6,;8,;10,;14,;20,;26,;34,;46,dots
]

Osservando i rapporti:

[
frac{L_{n+1}}{L_n}
]

Conway dimostrò che convergono a una costante detta di Conway [lambda_C approx 1.303577269ldots
]

Il fatto che emerga un invariante significa che sotto l’apparente caos opera una dinamica precisa: ogni termine è, in media, circa il 30% più lungo del precedente, indipendentemente dal punto in cui ci troviamo nella successione.
Non si può fare a meno di rilevare quanto la scoperta dell’esistenza di λ_C, un numero irrazionale, riproduca lo stesso sentimento di meraviglia che prese gli umanisti al cospetto della Divina Proporzione portati a dover prendere atto — contro ogni tradizione — che perfezione, bellezza, ordine sono paradossalmente legati a grandezze irrazionali.

Che le lunghezze, dopo i primi passi, risultino tutte pari è solo un effetto combinatorio della costruzione: non incide sulla complessità del processo né sul fatto che l’invariante ( lambda_C ) sia un numero irrazionale.

Ma c’è di più, quasi a suggerire un “Look and say” più generale sul mondo in cui viviamo e a ricordarci quanto superficiale sia la conoscenza che finora ne abbiamo: oltre alla presenza della costante ( lambda_C ), è possibile osservare la successione a un livello più fine, laddove cominciano a emergere frammenti ricorrenti, piccoli blocchi che ritornano in forme sempre più elaborate.

Per rendersene conto, guardiamo tre termini consecutivi della successione di seme 1, a partire da quando la struttura inizia davvero a organizzarsi:

( a_9 = 31131211131221 )
( a_{10} = 13211311123113112211 )
( a_{11} = 11131221133112132113212221 )

Se li osserviamo con attenzione, vediamo che iniziano a comparire blocchi ricorrenti.

Alcune sequenze corte, come 1131 e 1113, ritornano tra un termine e l’altro, mentre altre, come 3113 o 1311, emergono in una fase ma scompaiono in quella successiva. È come se la successione stesse sviluppando una propria grammatica di “sillabe”, alcune più stabili, altre meno.

A partire da (a_{10}) entra anche in scena un blocco più lungo, 132113, che ricompare chiaramente in (a_{11}) e continuerà a riemergere nei termini successivi. È una sorta di mattoncino ricorsivo, un segnale della struttura interna più profonda.

Queste ricorrenze mostrano, infatti, che la successione non cresce in modo caotico: sotto la superficie agisce una grammatica di blocchi, che si riproducono e si ricombinano secondo regole stabili. È il primo segno che la Look-and-say non è solo una curiosità combinatoria, ma un sistema dinamico dotato di una sua struttura.

Ed è precisamente da questa intuizione che nasce l’idea più profonda di Conway: ogni termine della Look-and-say può essere scomposto in un numero finito di “elementi” fondamentali, proprio come le molecole sono composte da atomi. Quanti elementi? Esattamente 92: un numero che ricorda da vicino quello degli elementi naturali della tavola periodica (secondo alcune classificazioni 92, secondo altre 94).

Questi elementi compaiono e si ricombinano secondo leggi stabili e rigorose, e la costante ( lambda_C ) — il ritmo di crescita delle lunghezze — nasce proprio da questa dinamica: è l’impronta numerica di una struttura nascosta. Non a caso, alcuni hanno descritto il lavoro di Conway come una vera e propria “chimica dei numeri”.

C’è un ultimo arcano: la costante ( lambda_C ) è la soluzione reale positiva di un polinomio irriducibile di grado 71, un grado sorprendentemente alto per una struttura nata da una semplice regola descrittiva. Jonathan Comes, in un recente articolo, ne riporta l’espressione per esteso: un’equazione lunga e articolata che da sola testimonia la profondità delle dinamiche interne della successione:

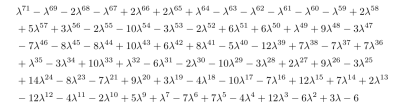
La sorprendente conclusione è che dietro una regola linguistica per bambini si nasconde un sistema complesso governato da leggi strutturali profonde.
Nel prossimo articolo incontreremo un’altra perla ricorsiva nata dalla fantasia di Conway e Hofstadter: una successione che sembra parlare il linguaggio della biologia più che quello dell’aritmetica.

L’articolo La successione ricorsiva “Guarda e dimmi” di Conway proviene da MATMEDIA.IT.