La potenza del pensiero matematico inconscio

Un classico da rileggere: La matematica può essere sognata di Biagio Scognamiglio (2021): illumina il rapporto tra sogno, razionalità e creatività matematica.

In un saggio profetico dell’ottobre 2021 Biagio Scognamiglio esplorava il rapporto tra sogno, inconscio e pensiero matematico, da Freud a Lacan, da Cartesio a Ramanujan. Alla luce delle attuali riflessioni sulla creatività matematica e sui processi cognitivi impliciti, vale oggi una nuova rilettura: non solo “se la matematica possa essere sognata”, ma che cosa della matematica continua a lavorare proprio quando dormiamo.

Qualche settimana dopo, sulle stesse pagine, Emilio Ambrisi tornava su quelle visioni notturne, ricordando come proprio dai tre sogni del 10 novembre 1619 Cartesio abbia tratto la rivelazione del metodo che condurrà alla nascita della geometria analitica — quella che Kasner e Newman chiameranno “la musica da programma della matematica”. Una notte agitata da immagini e simboli è diventata così, nella storia della scienza, un punto d’origine della matematica moderna.

Scognamiglio nel suo articolo riassume così i famosi tre sogni di Cartesio.

Il primo: al filosofo matematico appaiono fantasmi spaventosi che lo costringono a camminare in modo sbilenco;  un vento turbinoso lo fa girare su se stesso; egli cerca una chiesa per pregare, ostacolato dal vento che gli impedisce di salutare una persona e di ricevere da un’altra un dono, forse un frutto esotico; fra gli astanti tutti in piedi si sente costretto a restare curvo e traballante; si desta indolenzito e si rivolge alla misericordia divina per essere preservato dalle insidie di un demone maligno.

Il secondo: rimbomba un tuono; all’improvviso frastuono il filosofo matematico si desta e rimane in uno stato allucinatorio che gli fa vedere la camera invasa da scintille; tuttavia, riesce a distinguere gli oggetti e si persuade di non dover avere paura di alcunché.

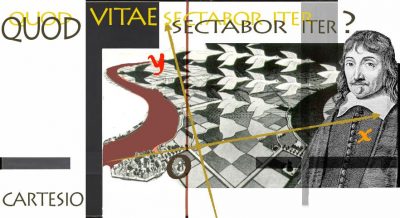
Il terzo: il filosofo matematico vede materializzarsi sul suo tavolo, senza sapere come, un Dizionario, lo sfoglia, ne è contento; gli appare poi misteriosamente un altro libro, un’antologia di poeti; la apre a caso; legge tra i versi l’interrogativo Quod vitae sectabor iter? e subito  dopo uno sconosciuto lo spinge a ricordare gli idilli di Ausonio citando l’inizio di un verso, Est et non;  allora cerca quegli idilli, trova il libro che dice di conoscere alla perfezione, spiega allo sconosciuto che non sa da dove l’abbia preso e aggiunge di aver trovato poco prima un libro misteriosamente sparito, che però riappare mutato nelle dimensioni.
Rivolge poi l’attenzione alla raccolta poetica in cui non trova  Est et non ma informa lo sconosciuto che ce n’è una più bella con l’incipit Quod vitae sectabor iter?, solo che non riesce a trovarla; cerca di giustificarsi dicendo che quell’antologia è di un’edizione diversa dalla sua; d’un tratto lo sconosciuto e i libri scompaiono. Questa volta Cartesio continua a dormire.

Per chi insegna matematica, rileggere oggi La matematica può essere sognata significa recuperare una dimensione spesso trascurata: la matematica come attività immaginativa, affettiva e simbolica, non solo logico-deduttiva.

I sogni di Cartesio, riletti da Scognamiglio e ripresi da Ambrisi, offrono un’occasione preziosa per ripensare la didattica: come nasce un’idea, quali processi inconsci la preparano, quali immagini interiori sostengono la comprensione.
Portare questa prospettiva in classe aiuta gli studenti a scoprire che la matematica non è solo procedura, ma creatività cognitiva, un campo in cui intuizioni, visioni e risonanze emotive hanno un ruolo reale. È un motivo in più per tornare a leggere — e far leggere — un testo che mira a restituire alla matematica molta della sua profondità umana.

L’articolo La potenza del pensiero matematico inconscio proviene da MATMEDIA.IT.