Cubiche, flessi e simmetrie
Una proprietà delle funzioni polinomiali di terzo grado. Approfondimenti e temi di maturità.
Per alcuni anni, agli esami di Stato, è stata proposta più volte la verifica della stessa proprietà delle funzioni algebriche razionali intere di terzo grado. Le formulazioni presentavano leggere differenze, come si può verificare nelle tracce seguenti.
- A. Si verifichi che la cubica di equazione ( y = x^3 + 3x^2 + 3x – 7 ) è simmetrica rispetto al suo punto di flesso. ( Quesito 7- Sessione straordinaria 2010 – PNI)
- B. Si dimostri che la curva di equazione ( y = x^3 + ax + b ) ha uno ed un solo punto di flesso rispetto a cui è simmetrica. . ( Quesito 6- Sessione ordinaria 2012 – PNI)
- C. Si dimostri che ogni curva di equazione ( y = x^3 + ax^2 + b x + c ) ha uno ed un solo punto di flesso, rispetto a cui è simmetrica ( Quesito 1- Anno scolastico 1997-1998 maturità magistrale – PNI)
- D. Si dimostri che il grafico di una qualsiasi funzione polinomiale di terzo grado ha esattamente un flesso ( Quesito 6 – Straordinaria 2012 – Ordinamento)
- E. In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), sono assegnate le curve di equazione
[
y=frac{1}{3}x^3 + kx – 3
]
ove (k) è un parametro reale. Dimostrare che tutte le curve passano per uno stesso punto A che per ciascuna di esse è punto di flesso e centro di simmetria. (Sessione ordinaria – Americhe 2005 -Problema 1 – Punto a)
In una prova d’esame più recente, nel Problema 1 della prova Straordinaria 2024, ritroviamo la stessa questione non più sintetizzata in modo essenziale, bensì articolata in più richieste che in essa convergono.
Problema 1 – Straordinaria 2024
Sia data la seguente funzione parametrica: ( y = x^3 + ax^2 + c.)
- Si dimostri che per ogni valore dei parametri reali (a) e (c) ((a neq 0)), il flesso coincide con il punto medio del segmento che ha per estremi i punti di massimo e di minimo relativi.
- Si determinino i valori dei parametri affinché la funzione abbia il massimo in (x= -2) e abbia un flesso di ordinata 6.
- Si disegni quindi il grafico della funzione ( f(x)=x^3+3x^2+4 ), e si calcoli l’area della regione finita di piano compresa tra la funzione, l’asse delle ascisse, l’asse delle ordinate e la retta di equazione (x = -2).
- Si dimostri infine che la funzione ( f(x) ) è simmetrica rispetto al suo punto di flesso.
- Successivamente, si applichi alla funzione ( f(x) ) la traslazione di vettore ( vec{v}(alpha,beta) ). Determinare ( alpha,betainmathbb{R} ), affinché la funzione traslata risulti dispari.
La frequenza con cui questo quesito è stato proposto, fa pensare che esso non rappresenti soltanto un esercizio di calcolo, ma possa acquistare una particolare rilevanza didattica. Tale proprietà, facilmente accessibile con gli strumenti dell’analisi elementare, permette allo studente di cogliere il legame tra concetti fondamentali – tangenza, concavità, studio locale di una funzione, molteplicità di intersezione tra una retta e una curva – e ancora: trasformazioni geometriche e invarianti , proprietà locali e proprietà globali di una curva..
Dimostrazione della proprietà
Con le procedure standard dei metodi analitici ( studio del segno della derivata seconda) si può dimostrare che la funzione ( y = f(x) = ax^3 + bx^2 + cx + d ) con (a neq 0) ha un solo punto di flesso (F(x_F , y_F)) con
[
x_F = -frac{b}{3a}
qquad
y_F = frac{2}{27}frac{b^3}{a^2} – frac{1}{3}frac{bc}{a} + d
]
La simmetria può essere verificata applicando le equazioni della trasformazione
[
begin{cases}
x = 2x_F -X \
y = 2y_F – Y
end{cases}
]
e provando che l’equazione della curva rimane invariata.
In alternativa si può trasformare la funzione assegnata con una traslazione che porti il punto (F) nell’origine O del riferimento e verificare che la nuova equazione rappresenta una funzione dispari (simmetrica rispetto ad O).
In particolare, il quesito A si risolve facilmente osservando che l’equazione della curva può essere scritta nella forma ( y = (x + 1)^3 – 8 ) e che, mediante la traslazione
[
begin{cases}
X = x + 1\
Y = y + 8
end{cases}
]
che porta il flesso di coordinate ((-1, -8)) nel punto (O(0,0)), l’equazione della curva assume la forma ( Y = X^3 ).
Approfondimenti
L’evidenza dei calcoli non deve celare la rilevanza dei risultati ottenuti o metterne in ombra l’aspetto concettuale. E’ importante , altresì, approfondire Il concetto di flesso e rispondere ad alcuni interrogativi:
- La presenza di almeno un punto di flesso è assicurata per quella particolare curva di ordine 3 o la proprietà si estende a tutte le cubiche? Perché, invece ogni conica ne è priva? Il numero dei flessi dipende dall’ordine della curva ? In che modo?
- Qual è il nesso tra la presenza di un punto di flesso (una proprietà di tipo locale) e la simmetria centrale della curva (proprietà globale)?
1. Definizione di flesso
Le funzioni polinomiali di grado (n) sono particolari funzioni analitiche ( di classe (omega) ) ma sono anche particolari curve algebriche di ordine (n). Possiamo prendere in considerazione, pertanto una duplice definizione di flesso che poggia su due proprietà caratterizzanti, collegate storicamente ai due principali problemi che portarono all’introduzione del calcolo differenziale: la definizione di retta tangente a una curva e la ricerca dei massimi e minimi di una funzione. L’una cura gli aspetti geometrici, l’altra l’aspetto analitico – funzionale.
Oltre alla consueta definizione di flesso «un punto di (f(x)) in cui (f”(x) = 0) e nel cui intorno si ha un cambiamento di convessità ( la tangente attraversa la curva e (f'(x)) ha un estremo locale )» esiste una definizione adottata nella teoria delle curve algebriche :
Data una curva algebrica (Gamma) di ordine (n) , dicesi flesso un punto non singolare di (Gamma) in cui la retta tangente incontra la curva con molteplicità di intersezione (ge 3).
In particolare, se (n =3), la retta del fascio avente per centro un punto (P) di (Gamma), non singolare, incontra ulteriormente la curva in 2 punti, contati con la loro molteplicità. La retta tangente in (P), pensata come posizione limite di una corda, è quella retta che incontra la curva in (P) con molteplicità uguale a 2. Il flesso è un punto speciale in cui l’intersezione curva-tangente ha molteplicità 3. Intuitivamente, la tangente inflessionale passa per il punto di tangenza e per altri due punti, appartenenti alla curva, infinitamente vicini.
Nel caso di una cubica polinomiale , dallo sviluppo di Taylor in un punto non singolare,
[
f(x) = f(x_0) + f'(x_0)(x-x_0) + frac{f”(x_0)}{2!}(x-x_0)^2 + frac{f”'(x_0)}{3!}(x-x_0)^3
]
e dall’equazione della retta tangente in un (P_0), ( y = f(x_0) + f'(x_0)(x-x_0)), si deduce che quest’ultima incontra la cubica in 3 punti coincidenti, se e solo se ( f”(x_0) = 0 ) e ( f”'(x_0) neq 0 ), cioè se (P) è un punto di flesso ( in accordo con l’altra definizione).
Legame con il centro di simmetria
a) Se la cubica di equazione ( y = f(x) ) è simmetrica rispetto a un suo punto, (P_0(x_0, y_0)),quest’ultimo è un punto di flesso.
b) Viceversa, se la cubica di equazione ( y = f(x) ) ha un solo punto di flesso (P_0(x_0, y_0)), quest’ultimo è anche centro di simmetria per la curva.
a) Se la tangente in (P_0) avesse contatto di ordine 2,il terzo punto di intersezione sarebbe un altro punto (Q neq P_0), ma ,per simmetria, retta e curva si dovrebbero incontrare anche in (P’), simmetrico di P rispetto a (P_0) . Ciò violerebbe il teorema Bézout (avremmo 4 intersezioni tra una retta e una cubica). Pertanto, le 3 possibili intersezioni sono assorbite in (P_0).
Un modo più intuitivo per giustificare il passaggio dalla proprietà globale (simmetria rispetto a un punto) a quella locale ( centro di simmetria coincidente con un punto di flesso) potrebbe essere questo: La simmetria rispetto a un punto (P_0) impone che ad ogni punto (Q), appartenente a un intorno di (P_0) , corrisponda un punto (Q’) tale che (overline{P_0Q} = overline{Q’P_0}). Al tendere di (Q) a (P_0) i tre punti tendono a sovrapporsi e la retta tangente avrà con la curva un’intersezione molteplicità uguale a 3.Pertanto (P_0) è un punto di flesso,
b) Viceversa, se la cubica di equazione ( y = f(x) ) ha un solo punto di flesso (P_0(x_0, y_0)),quest’ultimo è anche centro di simmetria per la curva.
Essendo ( f”(x_0)=0 ) e ( f”'(x_0)neq 0 ) lo sviluppo di Taylor nel punto (P_0) assume la forma
[
f(x) = f(x_0) + f'(x_0)(x-x_0) + frac{f”'(x_0)}{3!}(x-x_0)^3
]
ovvero
[
y-y_0 = f'(x_0)(x-x_0) + frac{f”'(x_0)}{3!}(x-x_0)^3
]
Poiché con la traslazione
[
begin{cases}
X = x-x_0\
Y = y-y_0
end{cases}
]
che porta (P_0) nell’origine del riferimento, l’equazione della curva diventa quella di una funzione dispari, ( Y = aX + bX^3 ), si deduce che (P_0) è centro di simmetria per la curva.
2. Numero minimo o massimo di flessi per una curva algebrica di ordine (n=3)
Una curva algebrica di ordine (nle 2) non può avere punti di flesso .
Il caso di un’equazione di primo grado, ovviamente corrispondente a una retta, non viene preso in considerazione nella ricerca dei flessi, poiché non si può parlare di cambiamento di convessità nell’intorno di un suo punto.
E’ nota, per una conica, la proprietà geometrica di non essere attraversata , in ciascun punto, dalla propria tangente. Come curva del secondo ordine, non può avere flessi in quanto la molteplicità di intersezione con una retta non può essere maggiore di 2.
Una cubica invece ha sempre almeno un punto di flesso e il passaggio al piano proiettivo complesso permette di determinarne il numero esatto.
Il numero massimo dei flessi di una cubica, nel piano proiettivo complesso , è uguale a 9. Questo è infatti il numero di intersezioni tra la cubica e la sua Hessiana che ha ugualmente grado uguale a 3.
La matrice hessiana (matrice delle derivate parziali seconde) di una cubica di equazione ( f(x,y,z)=0 ), in coordinate omogenee, è
[
begin{pmatrix}
f_{xx} & f_{xy} & f_{xz}\
f_{yx} & f_{yy} & f_{yz}\
f_{zx} & f_{zy} & f_{zz}
end{pmatrix}
]
Uguagliando a 0 il suo determinante si ottiene una curva di ordine 3, alla quale appartengono tutti i flessi della cubica ma anche i punti singolari, nodi o cuspidi.
All’annullarsi della curva hessiana corrisponde, infatti, una conica osculatrice degenere. Quest’ultima, nel caso di un punto singolare , si spezza nell’unione delle due tangenti principali (distinte o coincidenti), nel caso di un punto semplice ammette come componente la retta tangente, la quale viene ad avere un contatto superiore a 2 con la curva.
Ogni nodo assorbe 6 delle possibili intersezioni mentre una cuspide ne assorbe 8.
In generale, una curva algebrica irriducibile di ordine (n), possiede un numero di flessi uguale a (3n(n-2)-6delta-8k) dove (delta) è il numero dei nodi e (k) il numero delle cuspidi. Pertanto una cubica, nel piano proiettivo complesso, possiede 9 flessi se è non singolare, 3 flessi se ha un punto doppio nodale, 1 solo flesso se ammette una cuspide. Poiché le soluzioni complesse esistono sempre “a coppie” il numero dei flessi con coordinate reali è uguale a 1 oppure a 3.
I flessi di una cubica sono sempre a 3 a 3 allineati, cioè una retta che congiunge due flessi ne contiene un terzo. La proprietà è conseguenza dell’altra notevole proprietà dei tangenziali dei punti allineati ( essendo ogni flesso coincidente col suo tangenziale).
Poiché l’ordine di una curva e la molteplicità di intersezione sono invarianti proiettivi, nel piano proiettivo si possono definire, per le cubiche irriducibili, 3 classi di equivalenza
- La cubica non singolare
- La cubica nodale
- La cubica cuspidata
Alla terza classe appartiene la cubica di equazione (y=f(x)), proposta nei quesiti d’esame. La proprietà di possedere sempre uno e un solo punto di flesso acquista, pertanto, un carattere strutturale, dovuto alla presenza di un punto doppio cuspidale
E’ evidente che la suddetta curva è priva di punti singolari “al finito”, però si evince la presenza di un punto doppio coincidente con il punto improprio dell’asse (y), il quale assorbe due delle tre possibili intersezioni tra la curva e una generica retta verticale. Non essendo presenti rette asintotiche, la tangente in (Y_infty) è unica e coincide con la retta impropria , la quale ha con la curva un contato tri-punto.
In coordinate omogenee ((x,y,z)):
la soluzione del sistema è il punto di coordinate ((0,1,0)) con molteplicità uguale a 3.
Con un cambiamento di riferimento proiettivo si può trasformare la cubica e portare il punto singolare “ al finito”.
3.Trasformazioni affini e trasformazioni proiettive
Una qualsiasi cubica polinomiale che, come abbiamo visto, possiede un flesso-centro di simmetria, può essere ricondotta alla forma (y=x^3) mediante una opportuna trasformazione affine (una traslazione che porta il centro di simmetria nell’origine seguita da una dilatazione che elimina il termine di primo grado). In coordinate omogenee l’equazione diventa (yz^2 = x^3)
Applicando poi la trasformazione proiettiva
[
begin{cases}
X=x\
Y=z\
Z=y
end{cases}
]
otteniamo l’equazione
[
Y^2Z = X^3
]
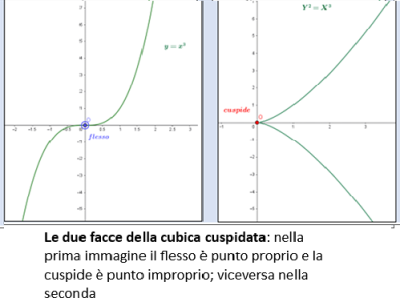
ovvero l’equazione della parabola semicubica col suo punto doppio cuspidale ben evidente nell’origine degli assi. La relativa tangente è la retta di equazione (Y=0) . Il flesso , inizialmente coincidente con il punto ((0,0,1)) si trasforma nel punto ((0,1,0)), punto improprio dell’asse delle ordinate , mentre la tangente inflessionale è la retta impropria (Z=0).
Le proprietà di avere una cuspide e un unico punto di flesso sono state conservate (proprietà proiettive), mentre non si ha più traccia della simmetria centrale (proprietà affine).
Interpretando la trasformazione come un cambiamento di riferimento proiettivo che scambia tra di loro l’asse delle ascisse con la retta impropria, si può osservare come alcune proprietà non siano caratterizzanti per la curva ma dipendono dal riferimento scelto.
E’ interessante osservare che nel nuovo riferimento la curva presenta una simmetria assiale, rispetto all’asse delle (x). Il risultato non è accidentale ma si spiega interpretando la simmetria centrale come una simmetria assiale con asse improprio
Equazioni della simmetria centrale in coordinate omogenee
[
begin{cases}
x’ = -x\
y’ = -y\
z’ = z
end{cases}
qquad
(x,y,0)to(-x,-y,0)equiv(x,y,0)
]
La trasformazione lascia fissa la retta impropria (z=0)
Scambiando la retta impropria con l’asse (x), quest’ultimo diventerà la retta unita (simmetria assiale).
4.Generalizzazioni
Per individuare le possibili generalizzazioni della proprietà delle cubiche polinomiali, è necessario prendere in considerazione:
- cubiche di diversa natura
- funzioni polinomiali di grado superiore a 3
- funzioni trascendenti
Dalle prove di maturità si può avere ancora qualche suggerimento per affrontare il problema dell’esistenza di un flesso e di un centro di simmetria in casi più generali. Nella più recente sessione d’esame è stato proposta una richiesta analoga, riferita però ad una funzione algebrica razionale fratta.
Quesito 8 straordinaria 2025. Dimostrare che la curva di equazione
[
y=frac{2x+1}{x^2+x}
]
è simmetrica rispetto al suo punto di flesso.
La funzione proposta può essere associata a una curva algebrica di ordine 3, di equazione (x^2y + xy – 2x – 1 = 0). Si tratta però di una cubica non riconducibile ad una di tipo polinomiale, come si riconosce studiandone i punti impropri. In questo caso la curva ha un punto doppio, improprio, di tipo nodale e dovrebbe presentare 3 punti di flesso. Si verifica infatti la presenza di due flessi le cui coordinate non sono numeri reali, automaticamente scartati nella soluzione standard. Traslando nell’origine il punto di flesso reale, si evidenzia la simmetria centrale della curva.
Problema 1. Suppletiva 1994. Studiare le funzioni: (y=x^3+1) e (y=sqrt{x^3+1}) e disegnare i loro grafici, rispettivamente (K’) e (K”), nello stesso piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy). Successivamente, tra i segmenti intercettati dalla regione piana R delimitata da (K’) e (K”) su una parallela all’asse (y), determinare quello di lunghezza massima. Calcolare infine il volume del solido generato da tale regione R quando ruota di un giro completo intorno all’asse (x).
La parte del testo che ci interessa è quella iniziale, dove si propone il confronto tra due funzioni , entrambe associabili a una curva algebrica del terzo ordine. La prima funzione è una cubica polinomiale, la seconda funzione è un ramo della curva ellittica (C) di equazione (y^2 = x^3 + 1).
La prima presenta una simmetria centrale rispetto al suo flesso, la seconda presenta una simmetria assiale ed ha 3 flessi reali, di cui uno improprio.
Il primo problema della sessione ordinaria (2013) PNI, tra le sue richieste, richiama l’attenzione sulla presenza di un flesso nella curva logistica, modello di crescita per un certo tipo di popolazione.
«Si supponga che f(x) costituisca, ovviamente in opportune unità di misura, il modello di crescita di un certo tipo di popolazione. Quali informazioni sulla sua evoluzione temporale si possono dedurre dai grafici in figura e in particolare dal fatto che (Gamma) presenta un asintoto orizzontale e un punto di flesso?»
L’equazione della curva assegnata è:
[
y=f(x)=frac{a}{1+e^{,b-x}},quad text{con } a=8 text{ e } b=2
]
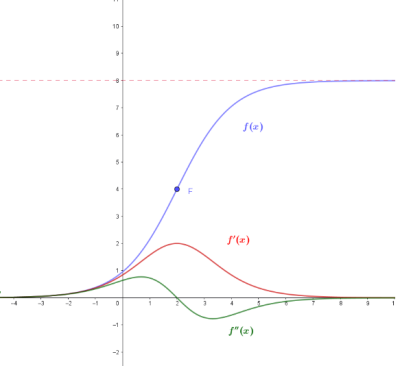Il flesso (F(2,4)) è interpretato nel suo significato fisico. E’ il punto in cui la velocità di crescita raggiunge il massimo valore per poi diminuire e tendere asintoticamente a 0. La sua ordinata è (a/2 = 4), dove (a) è la massima densità di popolazione sostenibile, corrispondente al valore cui tende la variabile (y) al tendere di (x) a (+infty) .
Anche in questo caso, però, è interessante verificare che (F) è centro di simmetria per la curva. Il processo, caratterizzato da una fase di crescita quasi esponenziale e da una fase in cui il ritmo è rallentato da fattori ambientali, acquista una specularità tra “passato e futuro”, forse poco realistica dal punto di vista naturale ma certo molto suggestiva.
Lo studio locale mediante lo sviluppo di Taylor permette di affrontare il problema del legame tra flesso e simmetria centrale nel caso più generale di una funzione (f(x)) che possa essere rappresentata dallo sviluppo in serie di Taylor, in un certo intervallo di convergenza.
Condizione necessaria e sufficiente affinché un punto di flesso (P_0(x_0,y_0)) di una funzione analitica (f(x)) ( non coincidente globalmente o localmente con una retta) sia anche centro di simmetria, è che (f(x)) ammetta uno sviluppo di Taylor
[
sum_{n=0}^{infty}frac{f^{(n)}(x_0)}{n!}(x-x_0)^n
]
nel quale compaiono solo potenze dispari del binomio ((x-x_0)), escluso il caso (n=0).
Solo in tal caso, infatti , una traslazione che porti (P_0) nell’origine trasforma la funzione in una funzione dispari.
Per le cubiche polinomiali la condizione si riduce all’annullarsi della sola derivata seconda; pertanto, il centro di simmetria è un flesso e viceversa.
Gli sviluppi in serie di Mac Laurin delle funzioni elementari confermano la validità della regola. Esempi
[
sin x = x – frac{x^3}{3!} + frac{x^5}{5!} – frac{x^7}{7!} + cdots
= sum_{n=0}^{infty}(-1)^n frac{x^{2n+1}}{(2n+1)!}.
quad text{Funzione dispari}
]
[
cos x = 1 – frac{x^2}{2!} + frac{x^4}{4!} – frac{x^6}{6!} + cdots
= sum_{n=0}^{infty}(-1)^n frac{x^{2n}}{(2n)!}.
quad text{Funzione pari}
]
[
e^x = 1 + x + frac{x^2}{2!} + frac{x^3}{3!} + cdots
= sum_{n=0}^{infty}frac{x^n}{n!}.
quad text{Funzione né pari ,né dispari}
]
Uno sguardo più attento al significato geometrico della simmetria negli esempi proposti rivela come simmetria centrale e simmetria assiale possano essere considerate proiettivamente equivalenti.
La verifica di queste proprietà e, soprattutto, la scelta di opportuni esempi e controesempi suggeriscono varie attività di indubbia valenza didattica.
Approfondimenti
L’articolo Cubiche, flessi e simmetrie proviene da MATMEDIA.IT.
Commenti