Dalla trigonometria alla goniometria

Prima la goniometria o prima la trigonometria? Una proposta alternativa ai percorsi canonici dei manuali scolastici.

Arrivati in quarta liceo, tutti i libri tendono a introdurre prima la goniometria, con la circonferenza goniometrica, definendo così seno, coseno e tangente. Poi si ricorda che seno, coseno e tangente sono anche proprietà geometriche dei triangoli rettangoli simili. Inoltre, anche con i teoremi della corda, dei seni e del coseno, si riescono a risolvere tutti i problemi con figure piane qualsiasi con tre o più lati: basta dividerle in triangoli. Inoltre la tangente si applica alla geometria analitica (il coefficiente angolare di una retta).

In realtà i docenti introducono l’uso trigonometrico di seno e coseno molto prima della trattazione in quarta liceo. In prima è necessario scomporre i vettori, in particolare le forze. In seconda si scompone il vettore forza (per calcolare il lavoro) ed il vettore velocità, almeno quella iniziale:
( vec{v}=vec{v}_x+vec{v}_y=(v_x,,v_y) ), scomposto appunto nelle componenti (v_x=vcdotcosalpha) e (v_y=vcdotsinalpha).
In terza si accenna alla circonferenza goniometrica per il moto circolare uniforme e per la connessione tra esso e il moto elastico, quindi si applica alle onde.

Ovviamente dipende dall’attenzione della classe, ma in genere si riesce a far vedere, magari con un’animazione Geogebra che il moto circolare uniforme (MCU) ha ascissa e ordinata di equazioni

Ovviamente le derivate, cioè la velocità e l’accelerazione, si affronteranno in quinta. Tuttavia credo sia interessante informare, già in terza, che il MCU e il moto armonico possono essere simultanei. Infatti già in terza, se non addirittura in seconda, si è parlato di velocità istantanea come rapporto di infinitesimi (ds/dt); nonché di accelerazione istantanea come rapporto di infinitesimi (dv/dt).

In terza i libri esprimono spesso anche la dizione derivata prima (dot{s}) per la velocità e la dizione derivata seconda (dot{v}=ddot{s}) per l’accelerazione, facendo notare che il secondo principio della dinamica si applica al moto armonico, che è vario:

A questo punto si può affermare che l’unica funzione che ha per derivata seconda l’opposto di se stessa, a meno di una costante moltiplicativa, è proprio la funzione coseno: (s=Acdotcos(omega t+varphi)).

È interessante far notare che, con (x=s), (A=r) e (omega^2=k/m), si ha la simultaneità tra il MCU ed il moto armonico sull’asse delle ascisse. Questo è ben visibile con un file Geogebra. Infatti (dot{s}=- ,omegacdotsin(omega t+varphi)), (ddot{s}=-A,omega^2cdotcos(omega t+varphi)=-omega^2 s) e, come detto, (ddot{s}=-frac{k}{m}s).

Ora arriviamo alla quarta. Qui non si può evitare la circonferenza goniometrica, se non altro per risolvere graficamente le equazioni e disequazioni goniometriche, in particolare quelle di primo grado (con una retta che interseca la circonferenza).

Anni fa ricordo che un testo dalla copertina rossa, con caratteri gialli, della Arnoldo Mondadori Scuola, in uno dei volumetti “Metodi e moduli di matematica” partiva dalla trigonometria. Infatti si possono definire le funzioni d’angolo seno, coseno e tangente a partire dalle relazioni dei triangoli rettangoli simili. Di seguito si possono dimostrare tutti i teoremi della trigonometria, l’identità goniometrica fondamentale e anche la formula di (sin(2alpha)=2,sinalpha,cosalpha).

Infatti basta disegnare una circonferenza e un triangolo rettangolo inscritto con base coincidente col diametro: l’altezza relativa ha di fronte sia l’angolo al centro (2alpha), che l’angolo del triangolo rettangolo inscritto (alpha). Eguagliando le due formule con il tipico sillogismo transitivo si ha: (rcdotsin(2alpha)=(2rcosalpha)cdotsinalpha).

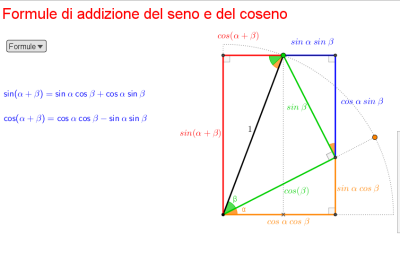
Anche le proprietà degli angoli associati possono essere dimostrate senza la circonferenza goniometrica. Tuttavia senza la dimostrazione di (cos(alpha-beta)) o (cos(alpha+beta)) non è possibile dimostrare le restanti formule goniometriche: questo è un passaggio obbligato nella costruzione teorica.

Alcuni libri propongono una dimostrazione interessante, alternativa a quella classica di (cos(alpha-beta)). Il libro sopra citato utilizza una circonferenza. Il Bergamini propone un contenuto digitale Geogebra interessante:

Anche questa, però, è comunque basata sulla circonferenza goniometrica. In attesa di scoprire se ci sono altre dimostrazioni, magari senza circonferenza, propongo un’alternativa.

Occorre disegnare un parallelogramma di lati (a) e (b), con un diagonale che individua due angoli acuti (alpha) e (beta). È necessario rilevare le eguaglianze riguardanti (h) in figura, perché serviranno nella dimostrazione.

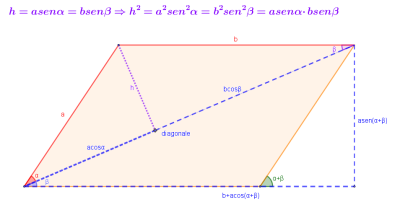
Quindi bisogna determinare un’uguaglianza, cioè descrivere la diagonale come somma di (acosalpha) e (bcosbeta), ma anche con il teorema di Pitagora (in alternativa si può usare il teorema del coseno):

Quindi, con un sillogismo transitivo, cioè eliminando il termine comune (text{diagonale}^2) si ha:

Ora si devono applicare le eguaglianze introdotte con la figura, cioè sostituire:
(a^2sin^2alpha=asinalphacdot bsinbeta) e (b^2sin^2beta=asinalphacdot bsinbeta) per ottenere:

Ossia la tesi, eliminando (2ab):

Dopodiché tutta la restante goniometria diventa un corollario … E la circonferenza goniometrica serve solo per descrivere meglio le equazioni e le disequazioni per via grafica.

L’articolo Dalla trigonometria alla goniometria proviene da MATMEDIA.IT.