In rete un’enciclopedia in latino: Vicipaedia. Tutta la matematica in latino: definizioni e teoremi, storia e personaggi.
Una scoperta sorprendente
Esiste in rete Vicipaedia, enciclopedia interamente in lingua latina, realizzata secondo le stesse regole di Wikipedia. Così viene accolto il visitatore:
“Bene advenisti in Vicipaediam! Vicipaedia est libera encyclopaedia, ad quam augendam omnes invitantur.”
Vi si trova espresso in latino tutto lo scibile.
Per ogni moderno termine specialistico è presente il suo corrispettivo latino. Un latino vivo non solo nel senso consueto di lingua dei classici ancora attuale, ma anche come lingua ben lungi dall’essere morta, capace com’è di esprimere i più vari aspetti dell’odierna civiltà.
Nella nostra scuola questa enciclopedia può offrire un utile apporto alla didattica, coinvolgendo docenti di diverse discipline e destando l’interesse degli studenti come già avviene per la sezione del nostro sito dedicata ai rapporti latino-matematica.
Da Vicipaedia stralciamo alcuni passi della voce Mathematica.
Il primo è una definizione in latino della disciplina. Segue ancora in latino il teorema di Pitagora. Riportiamo anche l’indice generale. Gli stralci successivi riguardano parte della storia della matematica e i rapporti matematica-filosofia. Dunque il latino è una lingua che ci parla dal passato, è voce del presente e si apre al futuro.
Il link per l’accesso a Vicipaedia è il seguente: la.wikipedia.org/wiki/Vicipaedia:Pagina_prima
Definizione della matematica in latino
Mathematica (-ae, f.) (Graece: ἡ μαθηματική (scil. ἐπιστήμη sive τέχνη) a voce μανθάνω ‘disco’)[1] sive mathematice[2] sive mathesis dicitur doctrinalis scientia, quae abstractam considerat quantitatem variis aspectibus, qui sunt algebraica, geometrica, analytica. Mathematica, quae fundamenta in numeris, logica, et ratiocinatione habet, est lingua physicae et aliarum scientiarum quantitativarum. De mathematica Galilaeus Galilaei scripsit:
“
Philosophia in hoc libro grandi scribitur, qui est universum semper nostris oculis oblatum. Hunc librum autem non possumus intellegere nisi imprimis eius linguam discere et litteras legere conamur. Liber lingua mathematica scriptus est et suae litterae sunt trianguli, circuli et aliae figurae geometricae. Eis litteris carentes haud singulam vocem librorum possumus intellegere; sine eis vagamur in labyrintho obscuro.
”
—Aequator Galilaeus Galilaei (Romae, 1623).[3]
Mathematica omnibus partium scientificarum essentialis est: scientiarum et naturalis et artificialis, medicinae, oeconomiae, scientiarum socialium. Sectiones mathematicae novae, ut mathematicae applicatae statistica et theoria ludorum, methodos mathematicas adhibendi cognoscunt. Hodie mathematica, tam necessaria in claves RSA securas creandas, partem magnam etiam agit in technologiis diversis, sicut in mercatura, communicationibus, televisionibus, et incolumitate interretiali vigilanda.
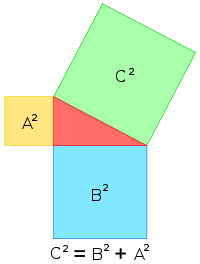
Teorema di Pitagora
Theorema Pythagorae, quod trianguli recti hypothenusam quadratam demonstrat aequalem esse summae aliorum laterum quadratorum. In aliis, quadratum in duo quadrata dividere potes.
Indice degli argomenti
Storia della matematica
Historia mathematicae brevis[recensere | fontem recensere]
Si plus cognoscere vis, vide MathematicusIn principio, mathematica creata est ut commercium facilius fiat: ad terram metiendam, ad pretia calculanda, et ad tales res quae sequuntur. Qua de causa in partes tres divisa est mathematica quae, e.g., ad mutationes, structuras spatiaque pertinent: analysis, algebra, geometria. Partes autem mathematicae per aetates variant ob nova reperta et scientiam processam.
Antiquitas[recensere | fontem recensere]
Aetate Romana, mathematica multas et diversas disciplinas cohibuit, sicut musicam et astronomiam, quas hodie ut mathematicales non habemus. Exempli gratia, Isidori Hispalensis saeculo septimo scripsit de mathematica:
Iam saeculo XVII, ut a Cartesii Newtonique verbis censamus, autem, soli mathematici dicuntur homines qui methodos novas colunt quantitativas.[5] […]
Matematica e filosofia
Mathematica et philosophia[recensere | fontem recensere]
Ob modicam mathematicae naturam, philosophi diu de mathematica sententias habere solent.[13] Plato putavit mathematicam referre formas ideales in altero mundo.
Thomas Aquinas tenuit mathematicam esse scientiam de his quae sine materia sensibile definiuntur sed, ut exsistant, materiam requirunt. Dedit exemplum de curvo et simo: simum includit in proprio definitione materiam sensibilem (i.e., nasum); curvum autem definiri potest sine sensibile materia particulare, sed in re non potest esse sine materia sensibile. Ita scripsit,[14] distinguens philosophiam naturalem a mathematica et metaphysica.[15] Quantitas, quae secundum Thomam dicitur accidens, potest sciri sine omnibus aliis entis formis, quia quantitates sunt communes inter omnes substantias materiales, antequam eae primum formantur, licet in modo potentiae propriae, non actu sint. Hoc amplius intelligibile est quia Thomas ipse docuit potentiam quantitatis praeintelligere in materia, ex dimensionibus non terminatis quae in materia insunt ante omnem formam.[16] Ergo mathematica, quae talibus quantitatibus studet, quoque sine sensibile materia particulare potest sciri.
In Immanuelis Kantii philosophia, mathematica constituebat unicam scientiae categoriam, de qua certi possumus esse, quod, secundum Kant, sola mathematica est synthetica a priori, quae de experientia non pendet.[17] Ayn Rand, quae Kantem vehementer opposuit, etiam de mathematica sententiam peculiarem habebat. In sua philosophia, omnis scientia, mathematica non excepta, ab experientia venit. Secundum Rand, omnes notiones veniunt ex actione qua magnitudines abstractiter a dimensionibus separamus. Haec actio a Rand dicitur magnitudines omittere.[18]
Altri aspetti della struttura di Vicipaedia
Aggiungiamo che sono dedicate voci specifiche ad algebra, geometria, statistica, matematica applicata; non mancano le biografie di matematici illustri; numerosi i link interni ed esterni, consistente l’apparato di note così come un elenco di fonti, vasta la bibliografia.
Il nostro saluto in latino ai lettori
A questo punto anche noi di Matmedia salutiamo i nostri visitatori con un augurio in latino.
Dilecte lector, utinam digito tuo, aut parvae machinae auxilio quae anglica lingua mouse dicitur, nexum premas quo Vicipaedia aditum suum omnibus praebet. Esto semper felix. Vale.