Una lezione di fine anno
Maturità scientifica. Una lezione di fine anno per la ricapitolazione e il potenziamento dei concetti e la preparazione all’esame. Ricapitolazione di analisi e geometria in vista della prova scritta della maturità
Questa attività si propone come sintesi di concetti e tecniche centrali dell’analisi matematica, in linea con quanto previsto dalla prova scritta dell’Esame di Stato. La funzione proposta consente di esercitare abilità di calcolo e di interpretazione grafica, ma anche di affinare la capacità di risolvere problemi geometrici con strumenti classici e analitici.
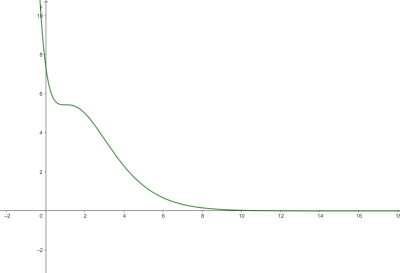
La funzione ( f(x) = (x^2 + 1)e^{-x+2} ) può essere interessante da proporre in classe quale spunto per questa attività di ricapitolazione di concetti e procedure importanti.
Il grafico della funzione è rapidamente ottenibile (Geogebra, ad esempio) e può essere fonte di numerose e utili osservazioni.
Ugualmente agevole è il calcolo della sua derivata prima:
[
f'(x) = (2x)e^{-x+2} + (x^2 + 1)(-e^{-x+2}) = (2x – x^2 – 1)e^{-x+2}
]
Meno immediato è trovarne una primitiva. Tuttavia, si può suggerire la funzione:
[
F(x) = (-x^2 – 2x – 3)e^{-x+2}
]
e verificare, tramite derivazione, che essa sia una primitiva di ( f(x) ):
[
F'(x) = (-2x – 2)e^{-x+2} + (-x^2 – 2x – 3)(-e^{-x+2}) = (x^2 + 1)e^{-x+2} = f(x)
]
Il problema
Sia ( f(x) = (x^2 + 1)e^{-x+2} ) definita per ogni ( x in mathbb{R} ) e sia ( r ) la retta di equazione ( y = frac{5}{2}x ).
Nel piano cartesiano, si consideri la regione ( R ) delimitata dal grafico (

