Trova l’intruso che non c’è
Mi ha commosso il modo in cui Christopher Danielson definisce il suo libro di 36 pagine intitolato Which one doesn’t belong? Playing with Shapes, 2016.
This book is different from many other books about shapes.
Every page asks the same question and every answer can be correct.
Questo libro è diverso da molti altri libri sulle forme. Ogni pagina pone la stessa domanda e ogni risposta può essere giusta.
Nel seguito vi proporrò alcuni esercizi ispirati alle idee di Christopher Danielson ma senza riprodurne direttamente i contenuti.
Tre esempi per cominciare
Ecco tre esempi risolti, per dare l’idea.
Esempio 1. Approccio banale
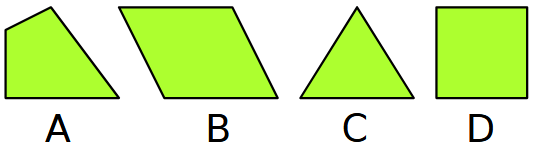
Quale forma non c’entra con le altre e perché?

Possibile soluzione
La figura è costruita per far notare facilmente che la forma C è l’unico triangolo mentre gli altri sono tutti quadrilateri. Quindi è irresistibilmente appagante concludere che l’intruso è C.
Facciamo un salto di qualità: inventiamo una situazione in cui ogni possibile terna ha una proprietà comune che il quarto elemento non ha.
Esempio 2. Figure piane
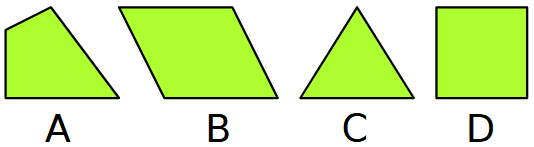
Quale forma non c’entra con le altre e perché?
Esamina ogni possibile terna di figure e trova una proprietà che esse hanno in comune ma che la quarta figura non ha.
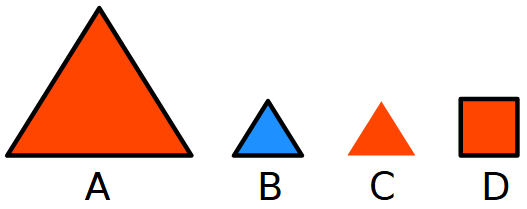
Possibile soluzione
- La A perché è grande mentre B, C, D sono piccole.
- La B perché è blu mentre A, C, D sono rosse.
- La C perché non ha il contorno mentre A, B, D lo hanno.
- La D perché è un quadrato mentre A, B, C sono triangoli.
Esempio 3. Numeri
Quale numero non c’entra con gli altri e perché?
Esamina ogni possibile terna di numeri e trova una proprietà che essi hanno in comune ma che il quarto numero non ha.
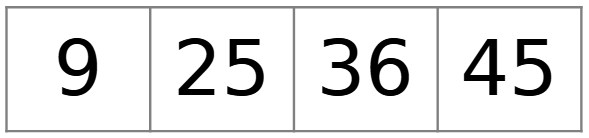
Possibile soluzione
- Il 9 perché è formato da una cifra mentre gli altri sono formati da due cifre.
- Il 25 perché la somma delle sue cifre è 7 mentre la somma delle cifre degli altri è 9.
- Il 36 perché è pari mentre gli altri sono dispari.
- Il 45 perché non è un quadrato mentre gli altri lo sono.
Appartenenza
Vi propongo ora altri esercizi su questa idea e vi invito a crearne di nuovi.
In inglese, si chiamano “Which is the odd one out?” oppure “Which doesn’t belong?”
The odd one out è l’eccentrico, colui che spicca perché ha qualcosa di diverso dagli altri.
To belong invece significa appartenere a un gruppo o stare in un certo contesto per una ragione specifica.
In Matematica si usa il simbolo ∈ per indicare l’appartenenza di un elemento a un insieme e certamente sapete che un insieme si può costruire in base a una proprietà comune dei suoi elementi ma si può anche definire in modo arbitrario.
Per risolvere questi esercizi bisogna trovare proprietà comuni degli oggetti con molta libertà e fantasia.
Esercizio 1. Figure piane
Quale forma non c’entra con le altre e perché?
Esamina ogni possibile terna di figure e trova una proprietà che esse hanno in comune ma che la quarta figura non ha.
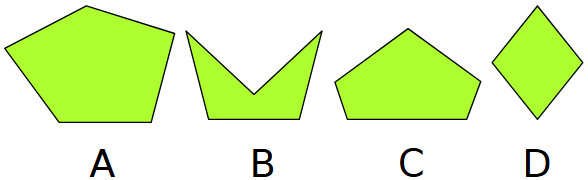
Guida alla ricerca delle soluzioni.
- Esamina le figure A, B, C. Trova una proprietà che esse hanno in comune ma che la figura D non ha.
- Poi esamina le figure A, B, D. Trova una proprietà che esse hanno in comune ma che la figura C non ha.
- Ripeti il procedimento con le figure A, C, D.
- Ripeti il procedimento con le figure B, C, D.
Esercizio 2. Figure piane
Quale forma non c’entra con le altre e perché?
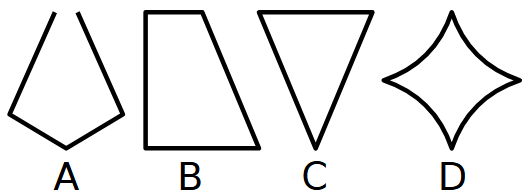
Esercizio 3. Numeri
Quale numero non c’entra con gli altri e perché?
Esamina ogni possibile terna di numeri e trova una proprietà che essi hanno in comune ma che il quarto numero non ha.
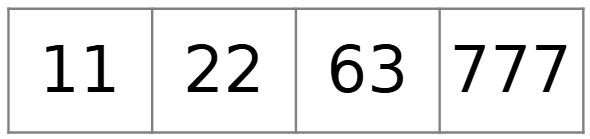
Esercizio 4. Numeri
Quale numero non c’entra con gli altri e perché?

Esercizio 5. Questa volta l’intruso c’è.
Quale forma non c’entra con le altre e perché?
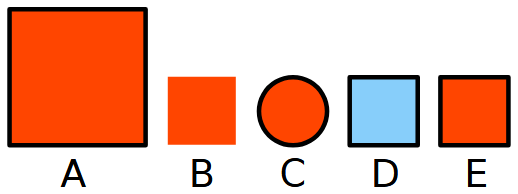
Nota. Questo problema è stato posto da Tanya Khovanova nel suo Tanya Khovanova’s Math Blog (lo trovate nell’archivio del 2009, datato 4 ottobre).
Esercizio 6. Numeri e fantasia
Quale numero non c’entra con gli altri e perché?
Puoi usare anche proprietà non strettamente matematiche!

E l’Intelligenza Artificiale, che ne dice?
Se volessimo chiedere all’Intelligenza Artificiale di inventare problemi come quelli che abbiamo visto, come dovremmo porle la domanda?
Questo potrebbe essere un esercizio interessante per noi umani!
Vi sottopongo qualche chicca e vi invito a provarci, sono certo che otterrete risultati migliori dei miei.
Prove con l’A. I. Copilot di Microsoft Bing.
Ha capito subito il testo seguente:
Trova un insieme di 4 numeri tali che ogni sottoinsieme di 3 numeri abbia una caratteristica comune che il quarto numero non possiede.
Purtroppo, anche dopo molti tentativi e segnalazioni di errori da parte mia, non è riuscito a inventare un esercizio corretto.
Ecco un esempio delle sue proposte.
|
Copilot. Provo con questa selezione: 3, 6, 9, 10. Ora verifichiamo le proprietà:
|
Prove con Perplexity.ai
La versione freemium di Perplexity.ai non ha capito bene la domanda seguente:
Trova un insieme di 4 numeri tali che ogni sottoinsieme di 3 numeri abbia una caratteristica comune che il quarto numero non possiede.
Ha fatto alcune prove e mi ha segnalato che la domanda è ambigua, ma dopo una breve discussione, è arrivato autonomamente a precisarla come segue.
|
Perplexity Grazie per la precisazione! Riassumendo la richiesta:
|
Tuttavia, neppure Perplexity è riuscito a inventare un esercizio corretto.
Da notare che ha usato proprietà composte, del tipo (pari oppure cubi).
Ecco un esempio.
|
Perplexity Un esempio di insieme è: {4, 8, 9, 27} con proprietà distinte per ogni terna, ad esempio:
|
Nella Matematica, oltre la matematica
Molti pensano che un problema di matematica dovrebbe essere chiaro, preciso, con tutte le informazioni necessarie e solo quelle, e avere una soluzione ben determinata e indiscutibile.
Questo va bene ma certamente non è il punto di partenza per chi vuole imparare a pensare come un matematico. E’ invece un traguardo da conquistare.
Giochi come “Trova l’intruso” sono divertenti e aiutano a sviluppare questo modo di pensare.
Ma se l’intruso non ci fosse? Forse la vera sfida non è trovare la risposta giusta, ma ripensare la domanda, per vedere le cose in modo diverso.
Tu mi chiedi di trovare l’intruso, ma io posso dimostrarti che nessuno lo è perché tutti hanno una proprietà speciale che gli altri non hanno e questa è a sua volta una proprietà di secondo livello che li accomuna, nessuno escluso.
Le nuove idee matematiche emergono da una nuvola, si chiariscono a poco a poco guardandole da vicino attraverso il ripensamento e la discussione.
A volte si rivelano diverse da da come sembravano all’inizio, altre volte rimangono aperte a più interpretazioni.
Questo è il modo in cui si impara la matematica e riflette anche la sua storia: un continuo gioco tra chiarezza e dubbi, regole e sorprese, domande e scoperte
Foto cover: Senorina_Irina / Shutterstock
Ilustrazioni: Gianfranco Bo
L’articolo è pubblicato anche su BASE Cinque.