L’approssimazione numerica scomparsa dalla maturità

L’esercizio che segue riguarda l’approssimazione e i metodi di approssimazione numerica. Un tema molto importante dell’istruzione matematica e, come tale, onnipresente nelle tracce delle prove scritte della maturità scientifica degli indirizzi sperimentali (quando c’erano). Un tema che negli ultimi anni non si ritrova più in nessuna forma: un’ulteriore grande perdita nella direzione dell’impoverimento progressivo della didattica della matematica.

L’esercizio si trova tra i quesiti della traccia assegnata nella sessione suppletiva del 2001.

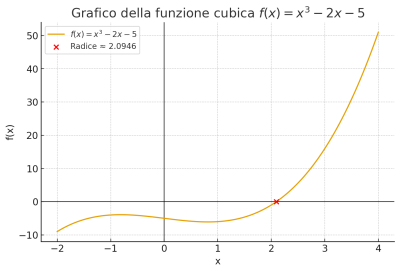
Verificato che l’equazione (x^3 – 2x – 5 = 0) ammette una e una sola radice compresa tra 2 e 3, se ne calcoli un’approssimazione applicando uno dei metodi numerici studiati.

1. Esistenza e unicità della radice

Da (f(x)=x^3-2x-5) segue (f(2)=-10). Per il teorema degli zeri esiste almeno una radice in ((2,3)).

Poiché (f'(x)=3x^2-2) e, su ([2,3]), (f'(x)>0), la funzione è strettamente crescente: la radice è unica e sta tra 2 e 3.

2. Metodi di approssimazione numerica a) Metodo di Newton

Scegliamo (x_0=2.5). La ricorrenza è

[
x_{n+1}=x_n-frac{f(x_n)}{f'(x_n)},qquad f(x)=x^3-2x-5,; f'(x)=3x^2-2.
]

Prime iterazioni:

(x_1 approx 2.164179) (x_2 approx 2.097135) (x_3 approx 2.094555) (x_4 approx 2.09455148)

Con tolleranza (10^{-6}): (;x approx 2.094551).

b) Metodo di bisezione

Dall’intervallo iniziale ([2,3]), dopo 10 bisezioni si ottiene

[
2.09375 ;< ;alpha ;<; 2.0947265625,
]

in coerenza con Newton (convergenza più lenta ma garantita).

c) Metodo delle secanti

Con (x_0=2), (x_1=3): (x_2approx 2.0588), (x_3approx 2.0811), (x_4approx 2.0909), … con convergenza verso la stessa radice reale.

3. Soluzione algebrica esatta: formula di Cardano a) Forma canonica (cubica priva del termine quadratico)

Continua la lettura su: https://www.matmedia.it/lapprossimazione-numerica-scomparsa-dalla-maturita/ Autore del post: Matmedia Fonte: http://www.matmedia.it