Simmetrie con i tetramini asimmetrici
In questo laboratorio di geometria useremo alcuni tetramini per cercare di costruire forme che abbiano uno o due assi di simmetria.
Gli obiettivi didattici principali sono:
- Vedere simmetrie assiali in situazioni non standard, cioè, per esempio, quando gli assi di simmetria non sono né orizzontali né verticali.
- Costruire forme simmetriche.
- Capire quanto è difficile mettere assieme pezzi asimmetrici per costruire una forma simmetrica, anche quando i pezzi sono pochi.
Per i nostri esercizi useremo i due tetramini asimmetrici che si chiamano L ed S e altri tetramini. Sono problemi classici, risolti da tempo, ma rimangono interessanti per chi li affronta per la prima volta.
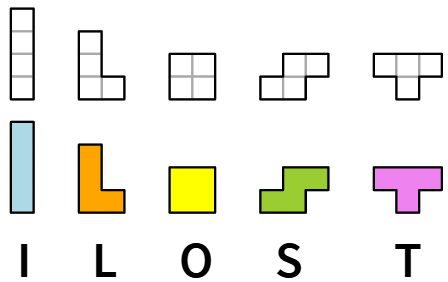
I nomi dei tetramini
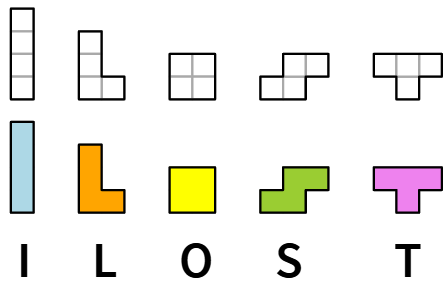
Per intendersi meglio, conviene dare un nome a ciascun tetramino. Ecco i nomi ufficiali.
Ci sono 5 tetramini distinti a meno di congruenze, cioè cioè traslazioni, rotazioni e riflessioni (o ribaltamenti) che si chiamano tetramini liberi.

I tetramini L ed S non hanno un asse di simmetria perciò, negli esercizi seguenti, dobbiamo distinguerli dalle loro immagini riflesse (o ribaltate).
Approfondiremo questo aspetto più avanti.
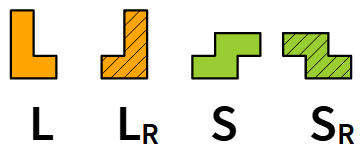
Oddity
Definizione. Una polyomino oddity è una figura piana con un asse di simmetria formata da un numero dispari (2n+1) di polimini.
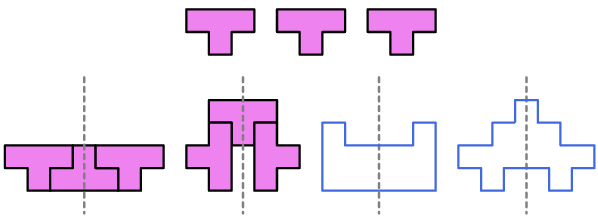
1. Con 3 T. Usando 3 tetramini T è possibile creare una forma con un’asse di simmetria?
Il tetramino T ha un asse di simmetria. Ci sono molte soluzioni ed è facile trovarle. Ecco alcuni esempi.
2. Con 3 L. Usando 3 tetramini L è possibile creare una forma con un’asse di simmetria?
Se necessario, si può ribaltare un tetramino.
Ci sono 2 soluzioni possibili.

Un piccolo suggerimento
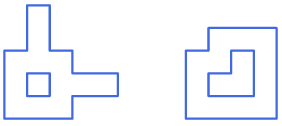
3. Con 5 L. Usando 5 tetramini L è possibile creare una forma con un’asse di simmetria senza buchi?
Se necessario, si può ribaltare un tetramino.

Un piccolo suggerimento

4. Con 5 pentamini L. Usando 5 pentamini L è possibile creare una forma con un’asse di simmetria?
Se necessario, si può ribaltare un pentamino. Questa costruzione è difficile.
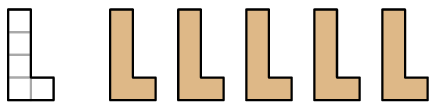
Un piccolo suggerimento
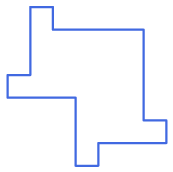
5. Con un numero dispari di S. Usando un numero dispari di tetramini S, è possibile creare una forma con un’asse di simmetria?
Questa costruzione, forse, è impossibile, ma provate comunque a realizzarla.
Semioddity
Negli esercizi precedenti, la oddity n. 5, forse è impossibile da realizzare.
Quando una oddity è impossibile, ci possiamo accontentare di una semioddity.
Definizione. Una polyomino semioddity è una figura piana con 2 assi di simmetria, formata da 2(2n+1) polimini.
Osservate che 2(2n+1) è un numero pari non multiplo di quattro.
6. Con 2 S. Create una forma con due assi di simmetria usando 2 tetramini S.
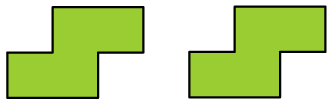
7. Con 6 S. Create una forma con due assi di simmetria usando 6 tetramini S.
Se necessario, si possono ribaltare alcuni tetramini. Questa costruzione è difficile.

Un piccolo suggerimento

PS: abbiamo pubblicato anche la soluzione!
Foto cover: stockmorrison / Shutterstock
Ilustrazioni: Gianfranco Bo
Questo articolo è tratto dal sito BASE Cinque, di Gianfranco Bo.

Commenti