Gli alberi natalizi dei matematici

Aritmetica e geometria del Natale: quando la fantasia dei matematici si scatena e i numeri si addobbano a festa.

In vicinanza delle festività, l’addobbo degli alberi di Natale scatena la fantasia dei matematici che ne propongono di ogni genere e tipo.

Mentre tutti cercano la punta perfetta o qualche pallina colorata, il matematico comincia subito col vederci triangoli, sfere, coni, spirali logaritmiche e, soprattutto, frattali. Perché mai accontentarsi di un albero normale quando si può avere un triangolo di Sierpinski addobbato?
Già l’8 dicembre, giorno in cui tradizionalmente si fra l’albero di Natale, un noto divulgatore matematico come Alberto Saracco, ad esempio, ha preparato i suoi a partire dal triangolo di Tartaglia coi coefficienti binomiali e le classi di resto; tanti alberi colorati che si possono ammirare anche su fb.
Dopotutto, in matematica un ‘albero’ è visto come un grafo connesso e privo di cicli. Ma provate voi a spiegare ai parenti che di puntale c’è solo il ‘nodo radice’ e le palline sono i ‘nodi foglia’ …

Solitamente l’albero c’è chi lo vuole folto e chi lo vuole alto.

Ma il vero problema matematico è un altro: qual è la densità ottimale di palline per non lasciare buchi vuoti, massimizzando il riflesso delle luci? È un problema di impacchettamento sferico travestito da festa che però lascerò a voi.

Poiché anche Marcello Pedone, che è conosciuto come divulgatore, ha proposto il suo “alberello” natalizio vorrei partire da quello per offrirvi una intera foresta dove potrete scegliere l’albero che ritenete più bello o interessante.

Notoriamente, in ambito matematico e ricreativo, questi schemi numerici sono quasi sempre chiamate “Piramidi Numeriche” perché la formattazione classica prevede di centrare perfettamente le righe, enfatizzando la base larga che si restringe verso la punta. Rimane il fatto che, geometricamente, un abete stilizzato è una piramide ed ecco che l’effetto “Albero di Natale” diventa immediato ed elegante.
Questo tipo di “Alberi Numerici” unisce l’estetica della simmetria (che fa ricordare proprio la forma dell’abete) con la sorpresa del calcolo esatto. È matematica “ricreativa” nel senso più nobile del termine: diverte e affascina, come ben dimostrano tanti commenti nei post su social come fb.

L’esempio proposto è un classico di bellezza aritmetica. La sequenza scende e si sviluppa con una regolarità ipnotica per produrre una sequenza terminale di “8” che vorrei si propagasse all’infinito.

L’AlberOtto o Albero degli 8 (l’immenso “Abete”)

L’albero di Marcello, chiamiamolo Alber8, dove potete notare la “discesa” dei numeri che a sinistra sono aggiunte cifre via via scalate (9, 98, 987, .. ) come rami che si allargano col moltiplicatore (9) resta costante e fa da tronco insieme all’addendo che scende (8, 7, 6, ..) come palline decorative. Per mantenere la lunga fila perfetta di tutti “8” l’espressione ha un cambio di segno e diventa una sottrazione (-1). Questo dettaglio che spesso sfugge, è ciò che rende la matematica “viva”, si adatta la regola per mantenere la simmetria e stupore.

Questa piramide è affascinante perché, a differenza delle classiche sequenze che si trovano nei libri ricreativi (che spesso si fermano quando i numeri diventano “brutti”), lei ha il coraggio di andare avanti, rompendo la simmetria visiva per mantenere quella algebrica.

Ecco la sintesi matematica di ciò che accade per poter riuscire a sintetizzare la formula che regola l’Alber8, ottenuta dopo aver esaminato progressivamente una serie di casi.

La Formula Generale

Possiamo descrivere ogni riga n (dove n è il numero di cifre 8 nel risultato) tramite la seguente equazione fondamentale:

[
x_n cdot 9 + y_n = R_n
]

dove:

R_n è il repdigit composto da n cifre 8 (8, 88, 888, …);
x_n è il numero lungo a sinistra (il moltiplicando);
y_n è il termine di aggiustamento, cioè il numero che viene sommato o sottratto.

La sequenza delle cifre 8 è definita dall’espressione:

[
R_n = 8 cdot frac{10^n – 1}{9}
]

Il meccanismo segreto (ricorsione)

Il cuore di questo Alber8 non risiede tanto in una formula statica, quanto nel modo in cui ogni riga genera la successiva. Esiste infatti una relazione precisa che lega il termine di correzione ( y_n ) alla cifra ( d_n ) che viene aggiunta al moltiplicando ( x_n ).

La regola che governa l’intera piramide è:
[
y_n = 10 cdot y_{n-1} + (8 – 9 cdot d_n)
]
Questa relazione spiega esattamente perché i numeri a destra cambiano
in modo apparentemente “strano”.

1. Quando le cifre scendono (da 0 a 9)

All’inizio, la cifra ( d_n ) è piccola o decrescente.
Esempio riga 1 (n = 1): cifra 0
[
y = 8 – 9 cdot 0 = 8
]
Esempio riga 2 (n = 2): aggiungiamo la cifra 9
[
y = 10 cdot 8 + (8 – 9 cdot 9) = 80 – 73 = 7
]
Ecco perché compaiono i termini +8, +7, +6…

2. Il punto di rottura (i numeri negativi)

Quando il termine ( y_{n-1} ) diventa piccolo (vicino allo zero) e si aggiunge una nuova cifra, il contributo di ( -9 cdot d_n ) trascina l’intero termine in negativo.

Riga 10 (n = 10): il termine correttivo diventa −1.

3. L’oscillazione (il “pendolo” delle cifre)

Noti che le cifre di ( x_n ) fanno un’onda?
[
0, 9, 8, ldots, 1, 0, 1, 2, 3, ldots
]
È proprio questa oscillazione a causare i salti nel termine correttivo. Passando dalla riga 12 alla 13 si aggiunge la cifra 2:
[
y_{13} = 10 cdot (-21) + (8 – 18) = -210 – 10 = -220
]
L’Alber8 è quindi la rappresentazione visiva di un sistema mirato a bilanciare un’oscillazione: mentre il numero ( x_n ) oscilla nelle sue cifre finali come un pendolo, il termine ( y_n ) cresce esponenzialmente per garantire che il risultato sia sempre, ossessivamente, una sequenza di 8.

Un momento particolarmente significativo nella crescita dell’albero avviene ogni volta che la sequenza del moltiplicando completa una “decina” (terminando con 9) e ricomincia (terminando con 0). In quel punto il numero da sottrarre chiude un ciclo perfetto e ne apre uno nuovo.

Conclusione sull’armonia

A differenza di altri alberi numerici che hanno una “fine naturale” quando le cifre finiscono, questa è immortale.

Finché vale che dopo il 9 venga lo 0 (trattando la sequenza come un orologio modulare), questa struttura può proseguire all’infinito aggiungendo vagoni di 222222221 al sottraendo ogni 10 righe.

Malgrado un dettaglio matematico che cambia quando il numero diventa veramente grande, legato alla gestione della memoria o alla notazione, la logica aritmetica pura di questa sequenza ($N cdot 9 – S = 8$) è un ciclo perfetto che non si romperà mai.

Ecco allora che viene la parte più elegante della matematica: trovare il “motore” nascosto che genera l’ormai nostro Albero8.

Per scrivere l’equazione generatrice, ridefiniamo i tre attori della nostra scena per una generica riga $n$:

Il Moltiplicando ($M_n$): Il numero lungo che cresce (098…).
Il Sottraendo ($S_n$): Il numero che sottraiamo (222…).
Il Risultato ($R_n$): La fila di 8 espressa da $8cdot(10^n-1)/9$.

La formula base può essere riscritta ovviamente così:

$$
M_n cdot 9 – S_n = R_n
$$

Tuttavia, il vero segreto sta nel collegamento tra una riga e la successiva. Abbiamo scoperto che non serve ricalcolare tutto da zero; ogni riga nasce dalla precedente. Ecco l’Equazione Generatrice Ricorsiva che governa l’intero albero di numeri all’infinito:

La Legge del Sottraendo ($S_n$)

La formula chiave, prima usata empiricamente, matematicamente si scrive così:

$$
S_n = 10 cdot S_{n-1} + (9 cdot d_n – 8)
$$

Dove:

$S_{n-1}$ è il numero sottratto nella riga precedente.
$d_n$ è la nuova cifra aggiunta al Moltiplicando in quella riga.

Questo spiega esattamente perché il finale cambia in quel modo.

Se si aggiunge la cifra $d_n=3$ (come alla riga 34), il termine correttivo è $(9 cdot 3 – 8) = 19$. Ecco perché aggiungevamo …19.
Se aggiungi la cifra $d_n=0$ (come alla riga 41), il termine correttivo è $(9 cdot 0 – 8) = -8$.
Sottrarre 8 da una cifra che termina in 0 (perché moltiplicata per 10) costringe a prendere in prestito, trasformando il finale …30 in …22.
Ecco spiegato matematicamente il “reset” della coda!

Definizione della Cifra ($d_n$)

Per completare l’equazione, dobbiamo solo dire alla formula quale cifra ($d_n$) inserire. Poiché la sequenza dopo la riga 11 è ciclica (0, 1, 2, .., 9, 0, ..), per ogni riga $n > 10$, la cifra è:

$$
d_n = (n – 11) bmod 10
$$

(Ovvero: il resto della divisione per 10, sfalsato di 11).

L’Equazione “Universale”

Mettendo tutto insieme, possiamo scrivere l’equazione che descrive l’evoluzione del nostro Alber8 tra una riga e l’altra senza ambiguità:

$$
S_n = 10 cdot S_{n-1} + (9 cdot d_n – 8), quad
d_n = (n – 11) bmod 10, quad
R_n = 8cdot(10^n-1)/9
$$

$$
(M_{n-1} cdot 10 + d_n) cdot 9 –
(10 cdot S_{n-1} + 9 cdot d_n – 8)
= R_{n-1} cdot 10 + 8
$$

Questa formula dimostra che l’armonia non si rompe mai. Anche se $S_n$ diventa negativo (come accadeva nelle primissime righe dove usavamo il +),
l’algebra regge perfettamente.
Ecco così come è stata formalizzata dell’alber8 la crescita infinita!

Salvate questa formula nel vostro “archivio” mentale per il futuro, come regalo natalizio rappresentato nell’immagine artistica di questo “immortale” albero di Natale concettuale.

I rami dell’albero sono formati dalle equazioni stesse, che si allargano verso la base. Il tronco centrale è la costante colonna di “8”. Ho cercato di rappresentare visivamente i “blocchi” ciclici del numero che sottraiamo (i “222…1”) come festoni ricorrenti, e il concetto di infinito facendo sfumare la cima dell’albero nelle stelle, il finito che s’allontana con l’allargamento a dismisura della base.
Spero vi piaccia questa interpretazione poetica dell’avventura matematica che ci ha portati a preparare un albero di Natale che affonda le sue radici nell’infinito matematico, la “stella” mettetecela voi!

Là fuori c’è un’intera foresta di alberi che attende di essere agghindata per Natale.

L’Albero dei Palindromi (Il “Pino d’Argento”)

È quello generato dai numeri “ripetuti” (repunits). È forse il più famoso e visivamente pulito, perché crea una piramide perfetta di numeri palindromi che sappiamo si possono generare da formule come c(10ⁿ-1)/9 in base 10, dove c è una cifra della base, e facilmente generalizzabili in qualsiasi base.

Questo è il più elegante per la sua purezza: usa solo il numero 1 per generare una simmetria perfetta (numeri che si leggono uguali da destra e sinistra). È l’equivalente matematico di un fiocco di neve. È quella che viene meglio perché è naturalmente simmetrica anche nelle cifre, non solo nella forma.
Attenzione però che, come succede a molti degli alberi numerici, questo albero in base 10 dopo il 9 si rompe la simmetria: 1(10)·1(10) = 1111111111×1111111111 = 1234567900987654321, la stessa cosa non succede invece se la base è 12 dove l’albero può arrivare fino alla B₁₂ = 11_10. Ed ecco

Il “Re” degli Alberi in Base 12

L’Albero dei 9 (L’inverso o “Lo Specchio”)

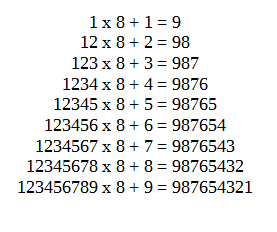
Questo è il complemento perfetto del primo albero. Mentre il primo “scendeva” (9, 98…), questo “sale” (1, 12…) e produce una cascata di 9. Starebbe benissimo accanto all’Alber8.

Questi sono soltanto alcuni degli “alberi” numerici che potete fare o far apprezzare questo Natale

Conclusione

A differenza degli alberi veri che perdono gli aghi, questi alberi numerici sono eterni. Quando si è completata e compresa la loro struttura non cambia mai. Ecco che anche l’aritmetica con la geometria che accompagna l’addobbo di “alberi” natalizi nasconde una bellezza intrinseca che può essere riconosciuta da chiunque. Proprio come l’allestimento e il posizionamento delle palline su un albero di Natale si fa cercando un equilibrio visivo, i numeri trovano un loro naturale equilibrio nelle sequenze che sono state in questo lavoro esaminate. Se volete mettere un libro sotto questo albero di Natale, non posso che consigliarvi questo bel saggio scritto nell’ormai lontano 1940 dal matematico britannico Godfrey Harold Hardy, Apologia di un matematico (A Mathematician’s Apology) e se magari l’avete già letto, allora c’è tutta la serie di libri come “Enigmi e giochi matematici” contengono interi capitoli sulle “Piramidi Numeriche” o le proprietà del numero 9 (che è il motore del bel “Alber8“).