Matematica con i triangoli
Fare matematica con i triangoli. Una formula ricorsiva per trovare i triangoli eroniani aventi lati espressi da numeri interi consecutivi.
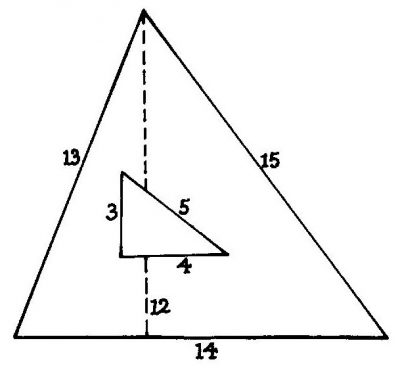
Il triangolo di lati 3, 4, 5 è particolarissimo. È l’unico con i lati, interi e consecutivi, ad essere rettangolo. Altrettanto particolare è il triangolo 13,14 e 15 che non è retto, ma è l’unico ad avere i lati e l’altezza espressi da numeri consecutivi: 12, 13, 14, 15. I due triangoli sono accomunati da un’ulteriore proprietà: hanno entrambi area razionale: 6 e 84.
Negli esempi presentati ci sono interessanti stimoli didattici ad andare avanti rafforzando concetti algebrici e geometrici. La considerazione cioè di triangoli aventi misure dei lati che siano numeri interi consecutivi si rivela molto promettente per fare matematica. La terna (1, 2, 3) è la più piccola possibile, ma non individua alcun triangolo. Un triangolo siffatto non esiste in quanto non sono soddisfatte le disuguaglianze di base. Esiste però il triangolo di lati 2, 3 e 4. Domanda: la sua area è razionale? Calcoliamola applicando la formula di Erone:
Essendo 9 il perimetro, è:
che non è razionale.
Il problema si può affrontare in termini generali: siano 2n, 2n-1 e 2n+1 i lati del triangolo. Allora il perimetro è 6n e l’area
che è razionale quando 3 (n2-1) è un quadrato perfetto.
Un punto di arrivo già notevole che è preludio altresì di uno sviluppo non meno interessante. Un aiuto in questo senso lo offre una formula scoperta da Henry Ernest Dudeney (1857- 1930) del quale si è già parlato in Triangoli con area e perimetro uguali.
 La formula di Dudeney è dn = 4dn-1 – dn-2 che ha il vantaggio di essere ricorsiva, un genere che piace agli studenti anche per il suo carattere operativo, del passo dopo passo. Chi è dn? È il numero centrale nelle due terne (3, 4, 5) e (13, 14, 15) considerate nell’ordine d1 = 4, d2 = 14. Allora: d3 = 4·14 – 4= 52 è il numero centrale della tripletta successiva e 4 · 52 – 14 = 194 e 4 · 194 – 52 = 724 sono i numeri centrali delle terne che vengono ancora dopo.
La formula di Dudeney è dn = 4dn-1 – dn-2 che ha il vantaggio di essere ricorsiva, un genere che piace agli studenti anche per il suo carattere operativo, del passo dopo passo. Chi è dn? È il numero centrale nelle due terne (3, 4, 5) e (13, 14, 15) considerate nell’ordine d1 = 4, d2 = 14. Allora: d3 = 4·14 – 4= 52 è il numero centrale della tripletta successiva e 4 · 52 – 14 = 194 e 4 · 194 – 52 = 724 sono i numeri centrali delle terne che vengono ancora dopo.
3 4 5
13 14 15
51 52 53
193 194 195
723 724 725
….. ….. …..
E le aree? Tutte razionali: 12, 84, 1170, 16296, 226974.
Il tema è interessante e notevole è la sua resa didattica in termini di profitto formativo. I docenti interessati ne trovano ampi riferimenti nella rete internet. In particolare: 536 Puzzles&Curious Problems edito da Martin Gardner nel 1967