Ancora una soluzione per il quesito 1
La prova scritta di matematica della sessione ordinaria 2023: ancora una soluzione analitica per il quesito 1. Quesito 1
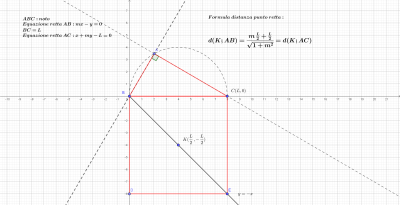
Sia ABC un triangolo rettangolo in A. Sia O il centro del quadrato BCDE costruito sull’ipotenusa, dalla parte opposta al vertice A. Dimostrare che O è equidistante dalle rette AB e AC.
Il quesito, di geometria euclidea, sembra aver interessato più i docenti e meno i candidati. Infatti, nelle stime lanciate da Serenella Iacino [VEDI] figura tra i meno affrontati dagli studenti. Paolo Francini, invece, gli ha dedicato un ammirevole e importante lavoro [VEDI]. Un “viaggio al centro del quadrato” in cui ha raggiunto la dimostrazione richiesta seguendo più vie. Dieci percorsi che attraversano ambiti diversi della matematica: quello della geometria sintetica e quello delle coordinate cartesiane, della trigonometria e poi dei vettori e infine quello dei numeri complessi. Una versatilità del quesito confermata altresì dalla soluzione data Antonino Giambò [VEDI] e quella che propongo ottenuta ragionando con le figure disegnate in ambiente Geogebra.
Ecco il foglio di lavoro che illustra, senza necessità di ulteriori specificazioni ( a parte la diversa denotazione del centro O), il processo dimostrativo seguito:

