La matematica come esplorazione-parte 2
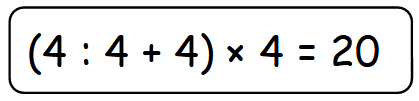
Care colleghe, cari colleghi, vi propongo la seconda parte dell’articolo pubblicato qualche settimana fa, completando così le cinque attività che aiutano a capire come funziona l’esplorazione in Matematica e come è collegata con l’immaginazione e la libertà. Sono adatte a diversi livelli scolastici, a partire dal secondo ciclo della scuola primaria.
Se affrontiamo queste attività con lo spirito dell’esplorazione matematica, arriviamo a sfiorare temi molto interessanti della ricerca contemporanea.
Questo articolo è una relazione dettagliata di un seminario che ho tenuto al 27o Convegno Nazionale “Incontri con la Matematica” – Castel San Pietro Terme (BO) – 2023. Le soluzioni delle attività di questa seconda parte saranno pubblicate nella prossima puntata. Ora riprendiamo da dove eravamo rimasti.
6. Esplorare un linguaggio formale: le espressioni aritmetiche
Le cosiddette espressioni aritmetiche sono forse l’unico caso meraviglioso in cui fin da bambini siamo messi a contatto con un linguaggio formale in piena regola. È bene quindi imparare non solo a risolvere le espressioni applicando le regole del calcolo, ma anche a costruire mini-espressioni esplorando le regole convenzionali del linguaggio.
Uno spunto interessante è il problema dei “Quattro 4” (Soares, 2020).
I QUATTRO 4
Roberto ha dimostrato come si possono usare quattro 4, le operazioni aritmetiche e le parentesi per ottenere 20.
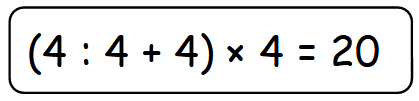
Utilizzando quattro 4, le operazioni matematiche che conoscete e le parentesi, siete capaci di ottenere tutti i numeri interi da 0 a 10?
Possibili momenti dell’esplorazione
- Si possono usare i “4” come cifre, per esempio 44 : 4 + 4 = 15.
- Si possono usare altre operazioni come il fattoriale (4! = 24), la radice quadrata (√4 = 2) .
- Si può usare il punto decimale all’inizio di un numero senza lo zero iniziale, scoprendo che 4 : .4 = 10.
- Si può usare la notazione con parentesi per indicare i numeri periodici, scoprendo che 4 : .(4) = 9.
- Si possono usare anche altri numeri diversi dal 4 e diversi fra loro.
- Si può costruire una procedura, eventualmente informatica, che permetta di trovare un insieme più o meno grande di risultati possibili.
- Si può riflettere su come si fa per darsi delle regole e poi estenderle, ridurle oppure cambiarle e controllare se sono accettabili oppure no.
7. Usare una variabile: quanti triangoli?
L’ultima proposta è ispirata da alcuni giochi sui triangoli pubblicati da Giovanni Filocamo (Filocamo 2022).
QUANTI TRIANGOLI CI SONO?
Osservate le figure.
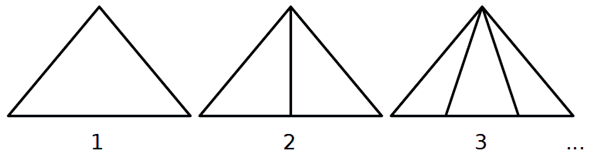
1. Quanti triangoli ci sono nella figura 1? E nella figura 2? E nella 3?
2. Se la sequenza continua con lo stesso criterio, quanti triangoli ci saranno nella figura n?
Possibili momenti dell’esplorazione
- Capire che la prima intuizione non sempre è quella giusta.
- Questo è anche un problema combinatorio: come possiamo essere sicuri di aver contato tutti i casi possibili?
- Cosa significa una lettera dell’alfabeto in una formula matematica?
- Perché è utile usare le lettere invece dei numeri in una formula matematica?
In molti casi (nella scuola di base), la prima risposta che viene in mente non è quella giusta. L’errore porta a esplorare gli aspetti combinatori del conteggio.
La seconda parte apre uno spiraglio verso il mondo della pre-algebra (sempre nella scuola di base), con l’uso della lettera che rappresenta un numero variabile.
8. Conclusione
Dicevo all’inizio che la cosa più importante per fare scoperte matematiche personali è l’atteggiamento da esploratore: non sai cosa troverai finché non parti, crea nuove possibilità, aspettati sorprese. Non importa se molti matematici sono già passati in quei luoghi. Ciò che importa davvero sono i tuoi passi sul sentiero che hai scelto e il tuo sguardo nel panorama che sta intorno.
In una soluzione i pezzi vanno solo ruotati, nelle altre invece un pezzo va ribaltato.
Bibliografia
Carey, B. (2014). Stanford’s Maryam Mirzakhani wins Fields Medal. Disponibile da: https://news.stanford.edu/2014/08/12/stanfords-maryam-mirzakhani-wins-fields-medal/
Da Ponte, J. P. (2005). Gestão curricular em Matemática. In GTI (Ed.), O professor e o desenvolvimento curricular (pp. 11-34). Lisboa: APM
Da Ponte, J. P., Branco, N., Quaresma, M. (2014). Exploratory Activity in the Mathematics Classroom. In Springer eBooks (pp. 103-125). Disponibile da: https://doi.org/10.1007/978-3-319-04993-9_7
Demaine, E., Korman, M., … Uno, Y. (2019). Symmetric Assembly Puzzles are Hard, Beyond a Few Pieces. arXiv:1703.02671v2
Filocamo, G. (2022). La matematica si impara giocando. Curiosità e giochi di intelligenza pensati per chi (non) ama la matematica.
Kitazawa, T. (2021). Arithmetical, Geometrical and Combinatorial Puzzles from Japan. American Mathematical Soc.
Soares, N. V., & Pirola, N. A. (2020). Resolução de problemas e expressões numéricas: o quadro dos quatro quatros e o nunca dois e números binários. REMATEC. Revista De Matemática, Ensino E Cultura, 15(35), 163–177. Disponibile da: https://doi.org/10.37084/rematec.1980-3141.2020.n15.p163-177.id291
Su, F. (2020). Mathematics for Human Flourishing. Yale University Press
Su, F. (2023). Matematica per il fiorire dell’essere umano. Carocci editore
Illustrazioni: Gianfranco Bo
Foto cover: peampath2812 / Shutterstock
Continua la lettura su: https://blogdimatematicaescienze.it/la-matematica-come-esplorazione-parte-2/ Autore del post: Fonte:
