Volume di un paraboloide di rotazione

La regola per calcolare il volume di un paraboloide di rotazione da Archimede a Guldino, a Cavalieri e al calcolo integrale.

Questo articolo è, sotto certi aspetti, connesso al precedente Area di un segmento parabolico, e come in quell’altro, l’autore fornisce la regola per il calcolo del volume di un paraboloide di rotazione e ne spiega la genesi e il relativo sviluppo, a partire dai primi risultati ottenuti da Archimede fino a quelli conseguiti con il ricorso al Calcolo Integrale.

La conclusione dell’articolo accenna ai due tipi di paraboloide non necessariamente di rotazione: ellittico e iperbolico, alle loro equazioni canoniche e alle loro costruzioni.

Per cominciare, cosa s’intende per “paraboloide di rotazione”?
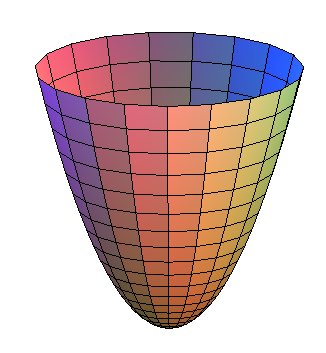
Assegnata una qualsiasi parabola p, di vertice V, la superficie S che si ottiene facendola ruotare di mezzo giro intorno al suo asse di simmetria si chiama paraboloide di rotazione.

Leggi l’articolo

Laureato in matematica presso l’Università di Messina. Ha insegnato matematica e fisica nei licei. Dal 1985 Dirigente superiore per i servizi ispettivi del MPI è stato responsabile della Struttura Tecnica Esami di Stato per il settore matematico e fisico. Ha tenuto corsi all’università e conferenze in numerosi convegni. È autore di saggi e libri di testo.

Visualizza tutti gli articoli .pp-multiple-authors-boxes-wrapper.pp-multiple-authors-layout-boxed.multiple-authors-target-the-content .pp-author-boxes-avatar img { width: 80px !important; height: 80px !important; } .pp-multiple-authors-boxes-wrapper.pp-multiple-authors-layout-boxed.multiple-authors-target-the-content .pp-author-boxes-avatar

Continua la lettura su: https://www.matmedia.it/volume-di-un-paraboloide-di-rotazione/ Autore del post: Matmedia Fonte: http://www.matmedia.it