Le trasformazioni geometriche nella didattica della Matematica
La presenza delle trasformazioni geometriche nella didattica della Matematica. Gli anni della matematica moderna e del PNI.
Il lento processo di rinnovamento dei programmi scolastici, avviato in Italia nei primi anni del dopoguerra, trovò un forte incentivo nei mutamenti culturali, politici e sociali nel passaggio dagli anni ’50 agli anni ’60.
Una tappa significativa per l’insegnamento della matematica, in campo internazionale, fu senz’altro il Seminario di Royaumont (23 novembre-4 dicembre 1959) organizzato dall’ OEEC (Organisation for European Economic Cooperation), in seguito divenuto OCSE.
Il dibattito era iniziato negli USA dopo il successo sovietico del lancio del primo Sputnik e riguardava la necessità di un insegnamento valido che potesse preparare adeguatamente i futuri tecnici e i futuri ricercatori. Com’è noto, infine si ebbe un vero e proprio cambio di paradigma sotto l’etichetta di “Matematica Moderna”.
Il grido “Abbasso Euclide! “ di Jean Dieudonné poteva essere interpretato come l’esigenza di una nuova assiomatica per agevolare il metodo dimostrativo, oppure come l’invito a conoscere i matematici meno lontani nei tempi e nei metodi, quali Cantor, Klein, Russell, Hilbert.
In realtà , l’evoluzione del pensiero matematico non solo metteva in luce l’inadeguatezza dei vecchi metodi d’insegnamento ma apriva nuovi scenari in ambito pedagogico e nelle ricerche sulla psicologia dell’apprendimento. Le principali scuole di psicologia ( Piaget, Bruner, Dienes) favorivano l’insegnamento basato sulla logica dei procedimenti matematici e più attento agli aspetti strutturali della disciplina.
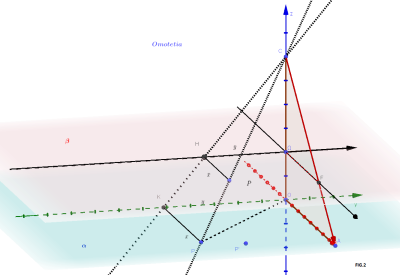
La teoria degli insiemi doveva essere assunta come base dell’aritmetica-algebra e le trasformazioni geometriche come base della geometria.
L’astrazione doveva
Continua la lettura su: https://www.matmedia.it/le-trasformazioni-geometriche-nella-didattica-della-matematica/ Autore del post: Matmedia Fonte: http://www.matmedia.it
