Simmetrie con i tetramini asimmetrici: risolto?
La settimana scorsa vi ho proposto un laboratorio di geometria in cui usare alcuni tetramini per costruire forme che abbiano uno o due assi di simmetria. Si tratta di problemi classici, che però rimangono interessanti per chi li affronta per la prima volta.
Li avete risolti? Ecco le soluzioni!
I nomi dei tetramini
Riprendiamo alcune definizioni.
Cos’è un tetramino?
Definizione per genere e differenza:
Un tetramino è un polimino formato da 4 quadrati.
Va bene, ma cos’è un polimino?
Un polimino è una forma geometrica composta da quadrati uguali uniti fra loro lungo almeno un lato.
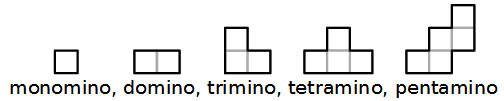
Così abbiamo il monomino, il domino, il trimino, il tetramino, il pentamino, e così via. Ecco alcuni esempi.

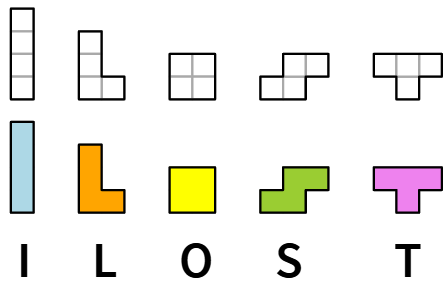
Quanti sono i tetramini liberi?
Provate a disegnare tutte le forme diverse che si possono ottenere usando 4 quadrati uguali uniti fra loro per almeno un lato.
Si ottengono 5 forme che si chiamano tetramini liberi.
Un tetramino libero è un tetramino considerato a meno di congruenze geometriche, cioè traslazioni, rotazioni, riflessioni (o ribaltamenti).
Cos’è la chiralità?
Osserviamo che i tetramini I, O, T rimangono uguali a se stessi quando vengono ribaltati cioè sono sovrapponibili alle loro immagini riflesse.
Invece L, S non sono sovrapponibili alle rispettive forme riflesse. Questa proprietà si chiama chiralità.
Una forma geometrica è chirale se non può essere sovrapposta alla sua immagine riflessa usando solo traslazioni e rotazioni.
I tetramini L ed S sono chirali.
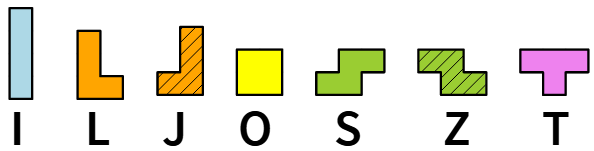
Quanti sono i tetramini unilaterali?
Se escludiamo la possibilità di riflettere (o ribaltare) un tetramino, allora otteniamo 7 tetramini unilaterali distinti. Questi tetramini sono quelli usati nel gioco del Tetris.
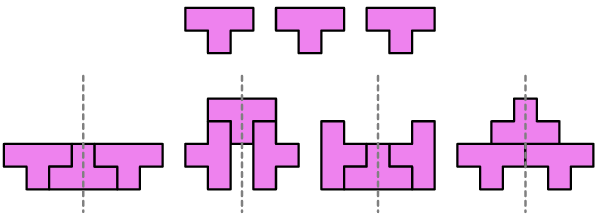
1. Con 3 T. Usando 3 tetramini T è possibile creare una forma con un’asse di simmetria?
2. Con 3 L. Usando 3 tetramini L è possibile creare una forma con un’asse di simmetria?
Se necessario, si può ribaltare un tetramino.
Ci sono 2 soluzioni possibili.
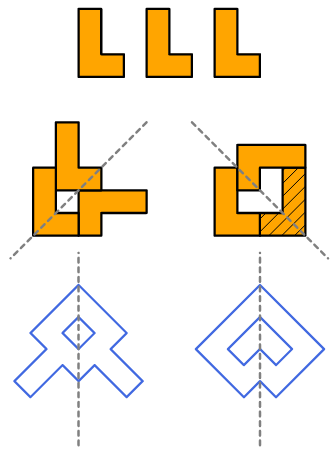
3. Con 5 L. Usando 5 tetramini L è possibile creare una forma con un’asse di simmetria senza buchi?
Se necessario, si può ribaltare un tetramino.
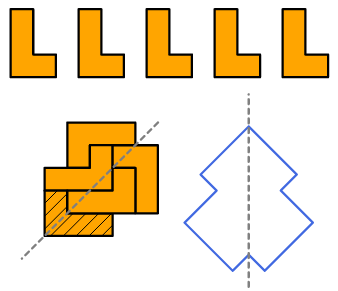
4. Con 5 pentamini L. Usando 5 pentamini L è possibile creare una forma con un’asse di simmetria?
Se necessario, si può ribaltare un pentamino. Questa costruzione è difficile.
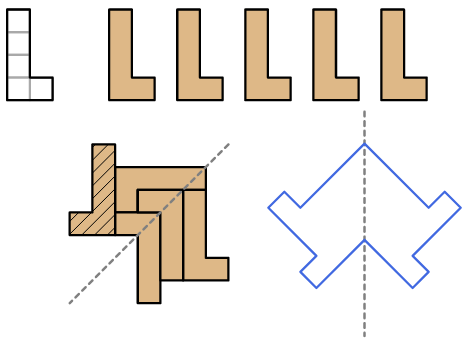
5. Con un numero dispari di S.Usando un numero dispari di tetramini S, è possibile creare una forma con un’asse di simmetria?
Questa costruzione, forse, è impossibile, non ho ancora trovato né una soluzione né una dimostrazione di impossibilità.
Semioddity
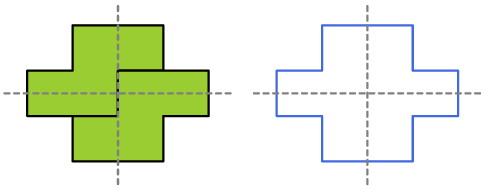
6. Con 2 S. Create una forma con due assi di simmetria usando 2 tetramini S.
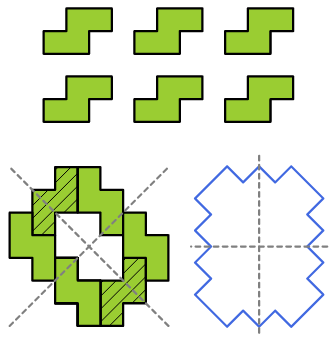
7. Con 6 S. Create una forma con due assi di simmetria usando 6 tetramini S.
Se necessario, si possono ribaltare alcuni tetramini. Questa costruzione è difficile.
Pace e bene a tutti
GfBo
Foto cover: stockmorrison / Shutterstock
Ilustrazioni: Gianfranco Bo
Questo articolo è tratto dal sito BASE Cinque, di Gianfranco Bo.
Continua la lettura su: https://blogdimatematicaescienze.it/simmetrie-con-i-tetramini-asimmetrici-risolto/ Autore del post: Fonte:

