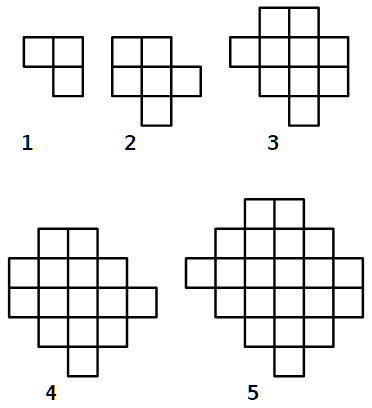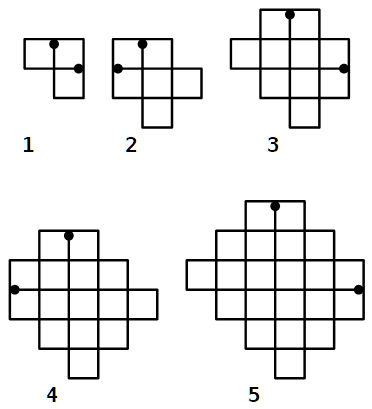Dopo la prima parte introduttiva con l’omaggio a Maryam Mirzakhani e la seconda parte con tre donne matematiche d’eccezione, in questa terza parte vi racconto delle ultime tre studiose che desidero omaggiare perché fonte di grande ispirazione nel nostro lavoro di insegnanti.
Claudia Zaslavsky
Grazie a Claudia Zaslavsky perché ci stimola a comprendere, rispettare e integrare il modo in cui ciascuna persona fa matematica, anche in relazione al gruppo culturale/etnico a cui appartiene.
Claudia Zaslavsky (1917-2006), etnomatematica statunitense
Cos’è la matematica?
Quando terminai l’Università ero convinto che la risposta a questa domanda dovesse essere uguale in tutto il mondo, da Napoli a Milano, dall’Italia alla Nuova Zelanda, dagli USA alla Nigeria.
Anni dopo, lavorando con alunni che provenivano da quattro continenti diversi (Europa, Africa, Sudamerica, Asia), mi resi conto che quella mia convinzione era assai limitante.
Fu così che incontrai l’etnomatematica e i suoi principali rappresentanti come Ubiratan D’Ambrosio, Gloria Gilmer e appunto Claudia Zaslavsky.
Solo per dare un’idea, elenco alcuni punti di collegamento tra gli studi etnomatematici e la didattica della matematica.
L’etnomatematica (ethno-mathema-tics) è lo studio delle tecniche matematiche utilizzate da gruppi culturali identificabili, con lo scopo di capire, spiegare e gestire problemi e attività che si presentano nel loro ambiente e nelle loro attività di lavoro.
Gli insegnanti dovrebbero tener conto di queste diversità, soprattutto quando lavorano in contesti multiculturali.
I curricoli scolastici dovrebbero tenere conto della natura multiculturale della società.
Non bisogna confondere la verità universale delle proposizioni matematiche con la base culturale della conoscenza. Per esempio, il teorema di Pitagora è lo stesso in qualunque luogo e tempo ma è costruito-dimostrato-raccontato-percepito in modi diversi nelle diverse culture.
Bisogna riconoscere e superare l’eurocentrismo (concezione occidentale) nell’insegnamento della matematica.
Bene, ma come mettere in pratica queste idee?
I libri di Claudia Zaslavsky contengono moltissime attività di matematica multiculturale adatte alla scuola di base.
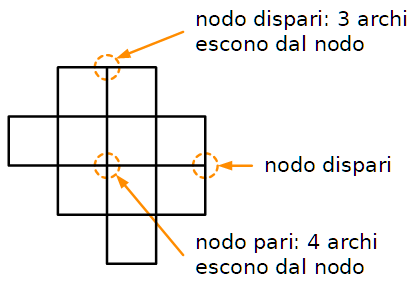
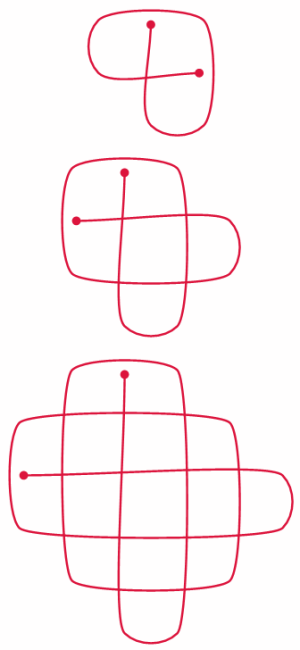
Eserciterai il tuo cervello risolvendo enigmi come il reticolo dei bambini africani di cui uno scienziato europeo ha detto: “È impossibile!”
Seguirai l’esempio di artisti islamici che hanno fatto bellissimi disegni usando solo la riga e il compasso.
Realizzerai modelli di case in cui vivono persone diverse in tutto il mondo.
In tutte queste attività userai la matematica. Una matematica a volte diversa da quella che impari a scuola.
Tratto e rielaborato da: Claudia Zaslavski, Math Games & Activities from around the World, 1998.
Qui cito soltanto i libri che mi sono stati particolarmente utili, tutti attualmente reperibili.
The Multicultural Math Classroom: Bringing in the World, 1995
Math Games & Activities from around the World, 1998
More Math Games & Activities from around the World, 2003
Number Sense and Nonsense. Games, Puzzles, and Problems for Building Creative Math Confidence, 2001, 2019
Africa Counts. Number and Pattern in African Cultures, 1999
Vi propongo qui un’attività tratta dal libro Multicultural Mathematics. Interdisciplinary Cooperative-Learning Activities, Claudia Zaslavsky, 1987,1993.
Claudia Zaslavsky è nota anche per la congettura secondo cui furono le donne a inventare la matematica.
La congettura Zaslavsky
Durante gli scavi archeologici presso il villaggio di Ishango (Congo) è stato trovato il più antico documento matematico: è un osso vecchio di 25.000 anni che riporta tre serie di incisioni che rappresentano numeri.
Chi ha inventato i numeri?
Ipotesi di Alexander Marshack: è un calendario lunare.
Claudia Zaslavsky: chi, se non una donna ha bisogno di un calendario lunare per tenere traccia del proprio ciclo mestruale?
Ipotesi maschilista: no, era sicuramente un agricoltore!
Claudia Zaslavsky: ok, sai chi ha inventato l’agricoltura? Le donne, mentre gli uomini andavano a caccia!
Quindi, in qualunque modo la si guardi, le donne sono state senza dubbio le prime matematiche!
Tratto e rielaborato da: Claudia Zaslavski, Women as the First Mathematicians, ISGEM Newsletter, Volume 7 Number 1, January 1992ISGEM = International Study Group on Ethnomathematics
Tanya Khovanova
Grazie a Tanya Khovanova perché ci insegna lo spirito dei circoli matematici russi e il valore della matematica ricreativa.
Tanya Khovanova
L’atmosfera della (didattica) matematica russa mi ha sempre affascinato, forse perché negli anni Settanta preparai alcuni esami di Analisi e Fisica studiando su libri russi tradotti in inglese. Li trovavo nella libreria Italia-URSS di Genova, dove un’intera stanza era dedicata alle pubblicazioni della casa editrice MIR. C’erano moltissimi libri di matematica di buona qualità a prezzi accessibili, per me.
Da quel momento cercai di seguire le attività dei Circoli Matematici Russi e in tempi più recenti ho scoperto il blog di Tanya Khovanova che è una miniera di informazioni preziose e magnifici problemi.
Non avevo successo come matematica perché continuavo a fare ciò che le persone mi chiedevano di fare.
Ma, alla fine, questo blog è stata un’opportunità per cambiare la situazione. Per la prima volta ho imparato a seguire il mio cuore. E il cuore mi ha portato alla matematica ricreativa: un mix di calcolo combinatorio, geometria, teoria delle probabilità e teoria dei numeri che assomiglia a un puzzle invece che alla matematica astratta.
Tratto da Emily Jia, To count the natural numbers, 2016 AWM Essay Contest: High School Level Winner
Non dobbiamo però dimenticare i numerosi episodi di discriminazione razzista messi in atto negli anni Settanta e Ottanta per impedire l’accesso di ebrei, armeni e altri studenti “indesiderati” al Dipartimento di Matematica dell’Università Statale di Mosca.
Tania Khovanova, assieme ad altri matematici come Edward Frenkel, Ilan Vardi e Jay Egenhoff, non ha esitato a testimoniare personalmente questo lato oscuro, per fortuna oggi superato.
Uno dei metodi usati per fermare gli studenti indesiderati era quello di assegnargli una serie diversa di problemi all’esame orale.Questi problemi erano progettati per avere soluzioni elementari (per evitare scandali) che però erano quasi impossibili da trovare.
Gli studenti che non riuscivano a rispondere potevano facilmente essere respinti.
Questi problemi in russo si chiamavano “problemi per ebrei” ed erano tenuti segreti.
Tratto e sintetizzato dall’articolo di Tania Khovanova e Alexei Radul, Jewish Problems, ArXiv, 2011 (arXiv:1110.1556v2)
Mi chiedevo se ci fossero dei vantaggi nell’educazione sovietica. Per prima cosa, i bambini sovietici crescono prima e sono meno ingenui. Sono più preparati per le dure realtà di quei ragazzi americani che sono privilegiati.
I bambini ingenui diventano adulti ingenui.
Gli adulti ingenui diventano presidenti ingenui.
Tratto dal Blog di Tanya Khovanova
Anna Cerasoli
Grazie ad Anna Cerasoli per insegnarci a svelare il senso della matematica attraverso la narrazione.
Anna Cerasoli
Beh, Anna Cerasoli si presenta da sola! È la più nota, prolifica e profonda scrittrice italiana di libri divulgativi di matematica per bambini e ragazzi.
Ha pubblicato oltre 20 libri di matematica narrativa, dal primo:
I magnifici 10. L’avventura di un bambino nella matematica, del 2001
al più recente:
Vacanze matematiche, del 2021.
I suoi libri si possono leggere a vari livelli. Consideriamo per esempio il racconto La grande invenzione di Bubal.
Bubal è una ragazza preistorica che ha ricevuto dal suo papà l’incarico di accudire bene le pecore senza perderne neanche una.
Per non correre rischi, la pastorella vorrebbe tenere le pecore sempre chiuse nel recinto ma quando l’erba finisce, deve affrontare un grande problema: come può scrivere con pochi segni la quantità delle sue pecore in modo da tenerle sotto controllo?
Bubal fa alcuni progressi parziali ma trova la soluzione definitiva attraverso un’illuminazione improvvisa dopo una notte di sonno ristoratore.
Ma alle prime luci dell’alba, eccola di nuovo sveglia.
…
A quel punto, un’idea illuminò la sua mente simile a un lampo in piena notte. Come non averci pensato prima?
Tratto da: Anna Cerasoli, La grande invenzione di Bubal, Emme Edizioni, 2012
All’arrivo dei tuoni il gregge era già al sicuro, sdraiato sotto il primo numero della storia, scritto da una bambina come voi.
Tratto da: Anna Cerasoli, La grande invenzione di Bubal, Emme Edizioni, 2012
Il collegamento con la congettura Zaslavsky è abbastanza evidente ma c’è anche un altro collegamento con le idee di Jacques Solomon Hadamard a proposito dell’invenzione in campo matematico.
Ho cercato di riassumere i risultati delle sue ricerche nello schema seguente.
Questo schema è uno strumento potente per allenare la propria creatività matematica ma bisogna capirlo, meditarlo, applicarlo.
Per approfondire l’argomento potete leggere il libro di Jacques Hadamard, La psicologia dell’invenzione in campo matematico, 1993, Raffaello Cortina Editore.
Stencil: rielaborazione grafica Gianfranco Bo