Nell’insegnamento della geometria alla scuola primaria, una delle nozioni fondamentali che i bambini imparano è il concetto di perimetro.
Comprendere il perimetro di una figura geometrica è essenziale per sviluppare le capacità matematiche dei bambini e prepararli per concetti più avanzati in futuro. Le schede didattiche semplificate sono uno strumento prezioso per gli insegnanti, poiché forniscono un modo efficace ed accessibile per introdurre e consolidare la comprensione del perimetro ai bambini.
In questo articolo, esamineremo l’importanza delle schede didattiche semplificate nell’insegnamento del perimetro alla scuola primaria e forniremo risorse utili per gli insegnanti e gli studenti.
A fine articolo potrete scaricare gratuitamente in formato PDF “I trapezi: Schede Didattiche Semplificate, Matematica per la Scuola Primaria“.
Indice
Cos’è il Perimetro e Perché è Importante
Prima di tutto, è importante comprendere cosa si intende per perimetro di una figura geometrica. Il perimetro è la somma delle lunghezze di tutti i lati di una figura. È un concetto fondamentale che permette di calcolare la lunghezza totale del contorno di una figura e viene utilizzato in diversi contesti matematici e pratici.
Utilizzo delle Schede Didattiche Semplificate per Insegnare il Perimetro
Le schede didattiche semplificate sono strumenti preziosi per gli insegnanti, poiché offrono una guida chiara e strutturata per l’insegnamento del perimetro. Queste schede contengono spiegazioni semplici e visivamente accattivanti del concetto di perimetro, esempi pratici e attività interattive che coinvolgono gli studenti nel calcolo del perimetro di diverse figure geometriche.
Calcolo del Perimetro per Figure Geometriche Comuni
Le schede didattiche semplificate presentano spesso esempi e esercizi che permettono agli studenti di calcolare il perimetro di figure geometriche comuni come quadrati, rettangoli, triangoli e cerchi. Attraverso esempi pratici e visivamente stimolanti, gli studenti possono comprendere meglio il concetto di perimetro e acquisire familiarità con le formule per il calcolo del perimetro di ciascuna figura.
Attività Pratiche per Apprendere il Perimetro
Oltre alla teoria, le schede didattiche semplificate offrono una varietà di attività pratiche che coinvolgono gli studenti nel calcolo del perimetro. Queste attività possono includere il disegno di figure geometriche e il calcolo del perimetro utilizzando cubetti o nastro metrico, la risoluzione di problemi di perimetro e il gioco con puzzle e labirinti che richiedono il calcolo del perimetro.
Conclusioni e Suggerimenti Utili
In conclusione, le schede didattiche semplificate sono uno strumento prezioso per insegnare il concetto di perimetro alla scuola primaria. Gli insegnanti possono massimizzare l’efficacia di queste risorse incorporandole nelle loro lezioni e adattandole alle esigenze specifiche dei loro studenti. È importante mantenere un approccio ludico e interattivo per stimolare l’interesse e l’entusiasmo degli studenti nell’apprendere il perimetro. Inoltre, è consigliabile incoraggiare il coinvolgimento attivo degli studenti attraverso attività pratiche e problemi di perimetro realistici che li mettano alla prova e li aiutino a consolidare le loro competenze matematiche.
Potete scaricare e stampare gratuitamente in formato PDF “Il perimetro: Schede Didattiche Semplificate, Matematica per la Scuola Primaria“, basta cliccare sul pulsante ‘Download‘:
Domande Frequenti su ‘Il perimetro’: Matematica per la Scuola Primaria
Quali sono le principali figure geometriche per le quali si calcola il perimetro nella scuola primaria?
Le principali figure geometriche per le quali si calcola il perimetro nella scuola primaria includono il quadrato, il rettangolo, il triangolo e il cerchio.
Come si calcola il perimetro di un quadrato?
Per calcolare il perimetro di un quadrato, si moltiplica la lunghezza di uno dei suoi lati per 4. In altre parole, il perimetro del quadrato è uguale alla lunghezza di un lato moltiplicata per 4 (P = 4 * l).
Come si calcola il perimetro di un rettangolo?
Per calcolare il perimetro di un rettangolo, si sommano le lunghezze dei quattro lati. Quindi, il perimetro del rettangolo è dato dalla somma delle lunghezze dei due lati lunghi e dei due lati corti (P = 2 * (lato lungo + lato corto)).
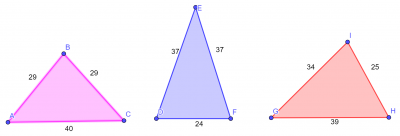
Come si calcola il perimetro di un triangolo?
Per calcolare il perimetro di un triangolo, si sommano le lunghezze dei tre lati. Non c’è una formula generale per il perimetro del triangolo, poiché può essere un triangolo equilatero (con tutti i lati uguali), isoscele (con due lati uguali) o scaleno (con tutti i lati diversi).
Come posso insegnare ai bambini della scuola primaria il concetto di perimetro in modo efficace?
Per insegnare ai bambini della scuola primaria il concetto di perimetro in modo efficace, è consigliabile utilizzare approcci pratici e manipolativi. Ad esempio, è possibile utilizzare materiali come i cubetti per costruire figure geometriche e calcolarne il perimetro in modo concreto. Inoltre, l’utilizzo di giochi e attività interattive può rendere l’apprendimento del perimetro più coinvolgente e stimolante per gli studenti.
Clicca per votare questo articolo!Maestra di Sostegno – Scuola Primaria