Grafico di una funzione tra regolarità e catastrofe
Modificare una funzione, evitare una catastrofe
Un contributo di Adriana Lanza tra matematica, fisica e didattica innovativa
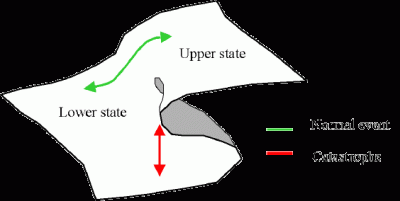
Catastrofe a piega
Con questo contributo dal titolo provocatorio – “Come modificare l’andamento di una funzione. Termini catastrofici per un grafico” – Adriana Lanza propone un’originale riflessione didattica sullo studio delle funzioni, rivolta in particolare agli studenti degli ultimi anni della scuola secondaria di secondo grado e ai loro docenti. Partendo da un’osservazione matematica stimolante – la presenza di un fattore di smorzamento nella funzione f(x) = (x² + 1)e−x+2 – l’autrice guida il lettore attraverso un percorso che intreccia matematica, fisica e pensiero critico. Il cuore del lavoro è rappresentato dalla distinzione tra trasformazioni geometriche – continue e prevedibili – e modifiche catastrofiche, in grado di alterare bruscamente le proprietà del grafico. Il riferimento alla teoria delle catastrofi di René Thom offre spunti interdisciplinari e stimola una visione dinamica dei grafici funzionali. L’autrice approfondisce poi due casi emblematici: L’oscillatore armonico smorzato: un classico della fisica meccanica che ben si presta a una rappresentazione analitica e visiva del concetto di smorzamento in un sistema dinamico. La catastrofe ultravioletta: esempio di “fallimento” della fisica classica risolto dalla legge di Planck, dove la funzione matematica viene modificata da un fattore esponenziale che evita la divergenza alle alte frequenze. Entrambi i casi mostrano come modificare una funzione significhi anche reinterpretare il fenomeno fisico sottostante. La matematica, così, diventa linguaggio e strumento per la comprensione critica della realtà. Approfondimenti allegati Un articolo che unisce
Continua la lettura su: https://www.matmedia.it/grafico-di-una-funzione-tra-regolarita-e-catastrofe/ Autore del post: Matmedia Fonte: http://www.matmedia.it
