Galilei agli esami di maturità

La scodella di Galilei e altri quesiti di matematica galileiana alla maturità scientifica per festeggiare i 400 anni del cannocchiale.
Il 2009 fu l’anno galileiano: 400 anni dall’utilizzo astronomico del cannocchiale (1609). Mi parve che il modo migliore di ricordare agli studenti la figura di Galileo Galilei fosse quello di fargli posto nei quesiti delle tracce di matematica degli esami di Stato. In effetti, una “strategia” ministeriale che aveva una lunga tradizione per il tema d’italiano e che per la matematica avevo proposto già nel 2006 per il centenario della nascita di Bruno de Finetti. Galilei fu in tal modo presente alla maturità scientifica con la sua scodella. Ma non solo!
Il quesito faceva parte di un insieme di cinque domande che svolgevano la funzione di anchor-item. Questioni basilari, cioè, proposte a tutti gli indirizzi, sia di ordinamento che sperimentali: concetto di funzione, solidi platonici, forme indeterminate, calcolo combinatorio, principio di Cavalieri. Tutte questioni care a Galilei. Potremmo dirle di matematica galileiana.
Vediamole in dettaglio:
- Sono dati gli insiemi
e
. Tra le possibili applicazioni ( o funzioni ) di A in B, ce ne sono di suriettive? Di iniettive? Di biiettive?
- “Esiste solo un poliedro regolare le cui facce sono esagoni”. Si dica se questa affermazione è vera o falsa e si fornisca una esauriente spiegazione della risposta.
- Si considerino le seguenti espressioni:
A quali di esse è possibile attribuire un valore numerico? Si motivi la risposta.
- Si dimostri l’identità
con n e k naturali e n > k
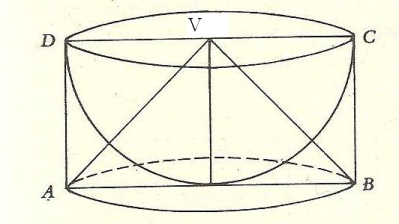 Nei “Discorsi e dimostrazioni matematiche intorno a due nuove scienze”, Galileo Galilei descrive la costruzione di un solido che chiama scodella considerando una semisfera di raggio r e il cilindro ad essa circoscritto. La scodella si ottiene togliendo la semisfera dal cilindro. Si dimostri, utilizzando il principio di Cavalieri, che la scodella ha volume pari al cono di vertice V in figura.
Nei “Discorsi e dimostrazioni matematiche intorno a due nuove scienze”, Galileo Galilei descrive la costruzione di un solido che chiama scodella considerando una semisfera di raggio r e il cilindro ad essa circoscritto. La scodella si ottiene togliendo la semisfera dal cilindro. Si dimostri, utilizzando il principio di Cavalieri, che la scodella ha volume pari al cono di vertice V in figura.
Perchè matematica galileiana?
Ci sono i solidi platonici, quelli che Keplero utilizzò per descrivere l’Universo:
«….Fra le orbite di Saturno e Giove ho messo il cubo, fra quelle di Giove e Marte il tetraedro, fra Marte e la Terra il dodecaedro, fra la Terra e Venere l’icosaedro, e lasciate che vi mostri….fra Venere e Mercurio il dodecaedro» e che Galileo incluse tra i caratteri nei quali è scritto il grande libro della Natura.
Ci sono il concetto di funzione e quello di infinito, il concetto di limite, gli indivisibili e il calcolo combinatorio. Sono argomenti tutti collegati.
Il concetto di funzione
Si può trovare questo concetto quasi ovunque nelle pagine dei Discorsi e dimostrazioni matematiche intorno a due nuove scienze, il libro in cui Galileo fondò la meccanica moderna. Galileo esprime le sue relazioni funzionali verbalmente e con il linguaggio delle proporzioni. Ad esempio: «Se un mobile scende, a partire della quiete, con moto uniformemente accelerato, gli spazi percorsi da esso in tempi qualsiasi […] stanno tra di loro come i quadrati dei tempi» e ancora: «I tempi impiegati a scendere su piani diversamente inclinati, purché però abbiano la medesima elevazione, stanno tra loro come le rispettive lunghezze».
Il linguaggio – scrive Morris Kline – mostra chiaramente che Galileo sta parlando di funzioni e mancava soltanto un piccolo passo per scrivere questi enunciati in forma simbolica. Poiché il simbolismo algebrico si stava allora estendendo, l’enunciato di Galileo sugli spazi descritti da un corpo che cade venne presto scritto nella forma s=kt2 e quello sui tempi di discesa nella forma t=kl.
Gli insiemi infiniti
Galileo dà il primo argomento serio per fornire una giustificazione al tabù dell’infinito attuale: se si fa corrispondere a ogni naturale n il suo quadrato n2, si definisce una biiezione tra l’insieme N e un suo sottoinsieme. Ma, dice Galileo, se ci fossero “tanti” quadrati quanti sono i numeri naturali, ciò violerebbe l’assioma che “il tutto è più grande della parte”; quindi non si può dire che i numeri naturali costituiscano un insieme! Galileo conserva il tabù aristotelico e non coglie quella distinzione che sarà fondamentale tra inclusione e equipotenza. Non sfugge al capestro:
«O, s’io mi sento in gamba esser ben destro
A varcar quel confin, perché al mio piede,
Poni il peripatetico capestro?»
Ma la definizione che ancora oggi si dà di insieme infinito l’ha ispirata proprio lui: un insieme E è infinito se esiste una biiezione tra E e un sottoinsieme A di E distinto da E.
La scodella
«Come si possa mai capire che un sol punto sia eguale ad una linea, vedendo di non ci poter far altro per ora, procurerò di quietare o almeno temperare una improbabilità con un’altra simile o maggiore, come talvolta una maraviglia si attutisce con un miracolo. E questo sarà col mostrarvi due superficie eguali, ed insieme due corpi pur eguali e sopra le medesime dette superficie, come basi loro, collocati, andarsi continuamente ed egualmente, e queste e quelli, nel medesimo tempo diminuendo, restando sempre tra di loro eguali i loro residui, e finalmente andare, sì le superficie come i solidi, a terminare le lor perpetue egualità precedenti, l’uno de i solidi con l’una delle superficie in una lunghissima linea, e l’altro solido con l’altra superficie in un sol punto, cioè, questi in un sol punto, e quelli in infiniti».
Galilei ha spesso pensato (qualcuno scrive dal 1610 in poi) alla composizione del continuo quindi agli infiniti, indivisibili e vacui. A questi temi non dedicherà uno scritto specifico, ma solo una “parentesi” della Giornata Prima dei Discorsi intorno a due nuove scienze a partire dal paradosso della scodella, ovvero: “Come si possa mai capire che un sol punto sia eguale ad una linea”.
Paradosso della scodella che porta il suo nome, ma qualcuno la dice di Luca Valerio (1552- 1618), accademico Linceo e professore al Collegio Romano sulla scorta di quanto egli stesso scrive: «Lasceremo per ora la dimostrazione, sì perché, volendola noi vedere, la troveremo nella duodecima proposizione del libro secondo De centro gravitatis solidorum posta dal Sig. Luca Valerio, nuovo Archimede dell’età nostra, il quale per un altro suo proposito se ne servì, sì perché nel caso nostro basta l’aver veduto come le superficie già dichiarate siano sempre eguali, e che, diminuendosi sempre egualmente, vadano a terminare l’una in un sol punto e l’altra nella circonferenza d’un cerchio, maggiore anco di qualsivoglia grandissimo, perché in questa consequenza sola versa la nostra meraviglia».
Infine il calcolo combinatorio che, a parte le notazioni introdotte più di un secolo dopo, Galileo aveva in particolare stima.
Italo Calvino così ne parla nelle sue Lezioni Americane:
“«Ma sopra tutte le invenzioni stupende, qual eminenza di mente fu quella di colui che s’immaginò di trovar modo di comunicare i suoi più reconditi pensieri a qualsivoglia altra persona, benché distante per lunghissimo intervallo di luogo e di tempo? Parlare con quelli che son nell’Indie, parlare a quelli che non sono ancora nati nè saranno se non di qua a mille dieci mila anni? E con quale facilità?
Con i vari accozzamenti di venti caratteruzzi sopra una carta».[…] Galileo vedeva nella combinatoria alfabetica («i vari accozzamenti di venti caratteruzzi») lo strumento insuperabile della comunicazione. Comunicazione tra persone lontane nello spazio e nel tempo, dice Galileo; ma occorre aggiungere comunicazione immediata che la scrittura stabilisce tra ogni cosa esistente o possibile […], il ragionamento istantaneo, senza passaggi: « Se il discorrere circa un problema difficile fosse come il portar pesi, dove molti cavalli porteranno più sacca di grano che un caval solo, io acconsentirei che i molti discorsi facessero più che un solo; ma il discorrere è come il correre, e non come il portare, ed un caval barbero solo correrà più che cento frisoni».
«Il discorrere è come il correre»: questa affermazione è come il programma stilistico di Galileo, stile come metodo di pensiero e come gusto letterario: la rapidità, l’agilità del ragionamento, l’economia degli argomenti, ma anche la fantasia degli esempi sono per Galileo qualità decisive del pensar bene.”
Il quesito sulla scodella risultò essere il meno affrontato. Il più difficile.
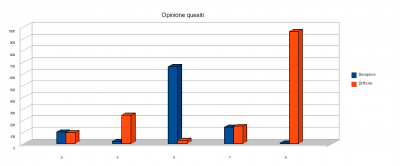
Al quesito della scodella tentò di rispondere poco più di un allievo ogni dieci. Un risultato disastroso anche in termini di qualità delle risposte. E c’è da dire che anche i docenti lo ritennero difficile e qualcuno addirittura attinente a questione “marginale”.
Si notò allora, a margine dell’Indagine Matmedia, quanto le questioni di geometria solida fossero sempre meno gradite principalmente ai docenti. Una conoscenza, dunque, che si correva il rischio di perdere, insieme ad altre, in una sorta di compensazione con altre ancora che forse si guadagnavano. Si osservò in definitiva, una generale perdita nelle abilità di risoluzione dei problemi, specie se riguardanti questioni di visualizzazione spaziale e di determinazione di luoghi geometrici, e si perdeva in ricchezza di significato. I nostri alunni sembravano disposti ad accettare sempre di più ricette su “come si fa” piuttosto che essere portati a considerare i perché e i ragionamenti sottesi. Come si calcola la derivata di una funzione o come si calcola un integrale sembravano riscontrare negli alunni maggiore disponibilità che ascoltare spiegazioni di cos’è una derivata o un integrale e del perché si fa così.
Ancora in quell’occasione si notò quanto l’Analisi fosse uno strumento potentissimo e che i professori agli esami di stato avrebbero voluto solo Analisi, in particolare lo studio di una funzione.
Ritornando a Galileo, egli compare ancora in un quesito del 2011.
Eccolo: “In una delle sue opere G. Galilei fa porre da Salviati, uno dei personaggi, la seguente questione riguardante l’insieme N dei numeri naturali ( “i numeri tutti”). Dice Salviati: «….Se io dirò, i numeri tutti, comprendendo i quadrati e i non quadrati, esser più che i quadrati soli, dirò proposizione verissima: non è così?». Come si può rispondere all’interrogativo posto e con quali argomentazioni?”
È la questione degli insiemi infiniti equipotenti discussa sopra. Anche per questo quesito i risultati furono molto deludenti.
RIFERIMENTI
Continua la lettura su: https://www.matmedia.it/galilei-agli-esami-di-maturita/?utm_source=rss&utm_medium=rss&utm_campaign=galilei-agli-esami-di-maturita Autore del post: Matmedia Fonte: http://www.matmedia.it

