Analisi indeterminata

Sull’analisi indeterminata. In particolare, le equazioni diofantee di primo grado in due variabili.

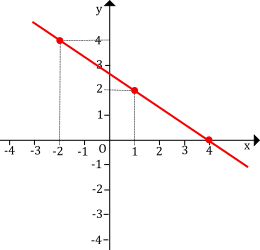
Nel piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), disegniamo la retta di equazione: 2x + 3y = 8. Ad essa appartengono anche punti a coordinate intere, come quelli evidenziati nella figura a lato.

Si pongono alcune domande:

• Esistono sulla retta altri punti le cui coordinate sono numeri interi?
• Ammesso che ne esistano altri, quanti sono complessivamente questi punti?
• Esistono formule idonee a determinare tali coordinate?

Quello di trovare le soluzioni espresse da numeri interi di un’equazione di primo grado in due variabili, è un problema che rientra in una tipologia di problemi concernenti la cosiddetta analisi indeterminata di primo grado.

L’articolo tratta questo tema della risoluzione delle equazioni diofantee di primo grado in due variabili. In particolare descrive un metodo basato sulle proprietà delle congruenze per la determinazione di una soluzione intera. Sono inoltre dimostrate le formule che forniscono tutte le soluzioni intere di un’equazione siffatta.

L’articolo